��Ŀ����
����Ŀ��ģ����Ӧ��.
��ģ�ͣ�
��1����ͼ������֪AB��CD����֤��1����MEN����2��360��.

��Ӧ�ã�
��2����ͼ�ڣ���֪AB��CD�����1+��2+��3+��4+��5+��6�Ķ���Ϊ ��
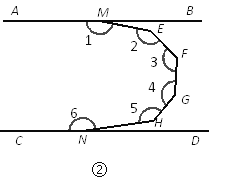
��ͼ�ۣ���֪AB��CD�����1+��2+��3+��4+��5+��6��������n�Ķ���Ϊ ��

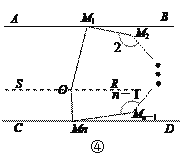
��3����ͼ�ܣ���֪AB��CD����AM1M2�Ľ�ƽ����M1 O���CMnMn��1�Ľ�ƽ����MnO���ڵ�O������M1OMn��m�㣮

�ڣ�2���Ļ����ϣ����2+��3+��4+��5+��6����������n��1�Ķ��������ú�m��n�Ĵ���ʽ��ʾ��
���𰸡���1��֤������������2��900�� ��180��(n��1)����3��(180n��180��2m)��
����������1������E��EF��CD������ƽ����ͬһֱ�ߵ�����ֱ����ƽ�пɵ�EF��AB��������ֱ��ƽ�У�ͬ���ڽǻ����ɵá�1����MEF��180�㣬��2����NEF��180�������ɵá�1����2����MEN��360�� ����2�����ֱ��E�㣬F�㣬G�㣬H����L1��L2��L3��L4ƽ����AB�����ã�1���ķ����ɵá�1+��2+��3+��4+��5+��6=180��5=900������������Ľ��ⷽ���ɵô𰸣���3������O��SR��AB������ƽ����ͬһֱ�ߵ�����ֱ����ƽ�пɵ�SR��CD��������ֱ��ƽ�У��ڴ�����ȿɵá�AM1O����M1OR����C MnO����MnOR�����ԡ�A M1O����CMnO����M1OR����MnOR�����ɵá�A M1O����CMnO����M1OMn��m�㣬���ݽ�ƽ���ߵĶ���ɵá�AM1M2��2��A M1O����CMnMn-1��2��CMnO���ɴ˿ɵá�AM1M2����CMnMn-1��2��AM1O��2��CMnO��2��M1OMn��2m�㣬�����A M1E����2+��3+��4+��5+��6����������n��1����CMnMn-1��180��(n��1)���ɴ˿ɵ�
��2+��3+��4+��5+��6��������n��1��(180n��180��2m)��.
��ģ�͡�
��1����ͼ������֪AB��CD����֤��1����2����MEN��360��.
֤��������E��EF��CD��
��AB��CD��
��EF��AB��
���1����MEF��180�㣬
ͬ����2����NEF��180��
���1����2����MEN��360��
��Ӧ�á�
��2��900�� �� 180��(n��1)
�ֱ��E�㣬F�㣬G�㣬H����L1��L2��L3��L4ƽ����AB�����ã�1���ķ����ɵá�1+��2+��3+��4+��5+��6=180��5=900�㣻
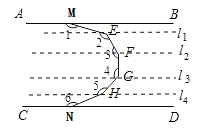
������Ľ��ⷽ���ɵã���1+��2+��3+��4+��5+��6��������n=180��(n��1)��
��3������O��SR��AB��
��AB��CD��
��SR��CD��
���AM1O����M1OR
ͬ����C MnO����MnOR
���A M1O����CMnO����M1OR����MnOR��
���A M1O����CMnO����M1OMn��m�㣬
��M1Oƽ�֡�AM1M2��
���AM1M2��2��A M1O��
ͬ����CMnMn-1��2��CMnO��
���AM1M2����CMnMn-1��2��AM1O��2��CMnO��2��M1OMn��2m�㣬
�֡ߡ�A M1E����2+��3+��4+��5+��6����������n��1����CMnMn-1��180��(n��1)��
���2+��3+��4+��5+��6��������n��1��(180n��180��2m)��

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�





