题目内容
【题目】如图所示，长方形ABCD是“阳光小区”内一块空地，已知AB＝（2a+6b）米，BC＝（8a+4b）米．
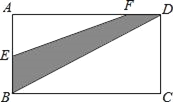
（1）该长方形ABCD的面积是多少平方米？
（2）若E为AB边的中点，DF＝
BC，现打算在阴影部分种植一片草坪，这片草坪的面积是多少平方米？
【答案】（1）16a2+56ab+24b2；（2）5a2+
ab+
b2
【解析】
（1）利用长方形面积计算公式即可求出答案；
（2）先求出AE、AF的长，再利用长方形面积的一半减去三角形AEF的面积即可得到阴影部分的面积.
解：（1）长方形ABCD的面积＝AB×BC
＝（2a+6b）（8a+4b）
＝16a2+56ab+24b2；
（2）由题意得，AF＝AD﹣DF＝BC﹣
BC＝（8a+4b）﹣（8a+4b）＝（6a+3b），
AE＝
（2a+6b）＝a+3b，
则草坪的面积＝×（16a2+56ab+24b2）﹣×AE×AF
＝×（16a2+56ab+24b2）﹣×（a+3b）（6a+3b）
＝5a2+ab+b2．
练习册系列答案
阅读快车系列答案
相关题目
