��Ŀ����
����Ŀ����ѧ���ϣ���ʦ�������������⣺
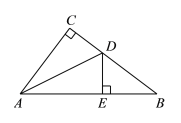
��֪����ͼ1����Rt��ABC�У���C=90�㣬AC=BC���ӳ�CB����D����DBE=45�㣬��F�DZ�BC��һ�㣬����AF����FE��AF����BE�ڵ�E��
��1����֤����CAF=��DFE��
��2����֤��AF=EF��
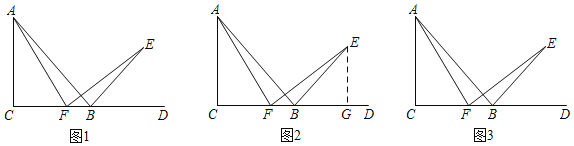
��������˼������ʦ��ͬѧ��С�齻����С��ͬѧ˵���˶��ڵڶ��ʵ��뷨��������ͨ�����캬�б�AF��EF��ȫ�������Σ�����ҹ���E��EG��CD��G����ͼ2��ʾ���������֤��Rt��ACF��Rt��FGEȫ�ȣ�����ͽ���ˣ�����������������֤��������ȵıߣ������������������в�ͨ����С��ͬѧ˵������Ȼ������������֤���������ٿ�����û���������Ӹ����ߵķ�����������˳��С��ͬѧ��˼·��ͼ3�м������ԣ�����ɣ�1������2���ʵ�֤����
���𰸡���1������������2��������
��������
��1�����ݡ�ͬ�ǵ������ȡ������ɵõ���CAF=��DFE��
��2����AC �Ͻ�ȡAG=BF������FG������ASA�����ж���AGF�ա�FBE�������ó�AF=EF��
֤������1���ߡ�C=90�㣬
���CAF+��AFC=90�㣮
��FE��AF��
���DFE+��AFC=90�㣮
���CAF=��DFE��
��2����ͼ3����AC�Ͻ�ȡAG=BF������FG��
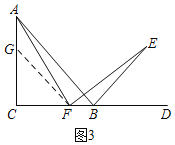
��AC=BC��
��AC-AG=BC-BF����CG=CF��
�ߡ�C=90�㣬
���CGF=��CFG=45�㣮
���AGF=180��-��CGF=135�㣮
�ߡ�DBE=45�㣬
���FBE=180��-��DBE=135�㣮
���AGF=��FBE��
�ɣ�1���ɵã���CAF=��DFE��
���AGF�ա�FBE��ASA����
��AF=EF��