题目内容
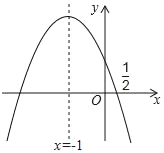
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
【答案】①②④
【解析】
首先根据抛物线![]() 的开口方向、对称轴及抛物线与y的交点可判断出a、b、c的符号,可确定①的正误;然后根据抛物线的对称轴为x=-1和抛物线与x轴的交点,可分别推得②③④⑤的正误.
的开口方向、对称轴及抛物线与y的交点可判断出a、b、c的符号,可确定①的正误;然后根据抛物线的对称轴为x=-1和抛物线与x轴的交点,可分别推得②③④⑤的正误.
①由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
②∵抛物线![]() 的对称轴是x=-1.且过点(
的对称轴是x=-1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(![]() ,0),
,0),
当x=![]() 时,y=0,即
时,y=0,即![]() =0,
=0,
整理得:25a-10b+4c=0,故②正确;
③直线x=-1是抛物线![]() 的对称轴,所以
的对称轴,所以![]() =-1,
=-1,
解得b=2a,
∴a-2b+4c=a-4a+c=-3a+c.
∵a<0,
∴-3a>0.
∵c>0,
∴-3a+c>0.
即a-2b+4c>0,故③错误;
④∵x=-1时,函数值最大,
∴a-b+c![]() (m≠1),
(m≠1),
∴a-b![]() m(am-b),所以④正确;
m(am-b),所以④正确;
⑤∵x=1时,y<0,
∴a+b+c<0,
∵b=2a,a=![]()
∴![]() +b+c<0
+b+c<0
∴3b+2c<0,故⑤错误.
故答案为:①②④.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目