Question

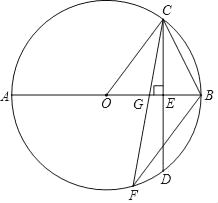
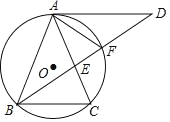
【题目】如图，△ABC内接于⊙O，AB＝AC，∠BAC＝36°，过点A作AD∥BC，与∠ABC的平分线交于点D，BD与AC交于点E，与⊙O交于点F．

(1)求∠DAF的度数；

(2)求证：AE2＝EFED；

(3)求证：AD是⊙O的切线．

Answer 1

【答案】(1)∠DAF＝36°；(2)证明见解析；(3)证明见解析.

【解析】

（1）求出∠ABC、∠ABD、∠CBD的度数，求出∠D度数，根据三角形内角和定理求出∠BAF和∠BAD度数，即可求出答案；

（2）求出△AEF∽△DEA，根据相似三角形的性质得出即可；

（3）连接AO，求出∠OAD=90°即可．

(1)∵AD∥BC，

∴∠D＝∠CBD，

∵AB＝AC，∠BAC＝36°，

∴∠ABC＝∠ACB＝×(180°﹣∠BAC)＝72°，

∴∠AFB＝∠ACB＝72°，

∵BD平分∠ABC，

∴∠ABD＝∠CBD＝∠ABC＝×72°＝36°，

∴∠D＝∠CBD＝36°，

∴∠BAD＝180°﹣∠D﹣∠ABD＝180°﹣36°﹣36°＝108°，

∠BAF＝180°﹣∠ABF﹣∠AFB＝180°﹣36°﹣72°＝72°，

∴∠DAF＝∠DAB﹣∠FAB＝108°﹣72°＝36°；

(2)证明：∵∠CBD＝36°，∠FAC＝∠CBD，

∴∠FAC＝36°＝∠D，

∵∠AED＝∠AEF，

∴△AEF∽△DEA，

∴，

∴AE2＝EF×ED；

(3)证明：连接OA、OF，

∵∠ABF＝36°，

∴∠AOF＝2∠ABF＝72°，

∵OA＝OF，

∴∠OAF＝∠OFA＝×(180°﹣∠AOF)＝54°，

由(1)知∠DAF＝36°，

∴∠DAO＝36°+54°＝90°，

即OA⊥AD，

∵OA为半径，

∴AD是⊙O的切线．