Question

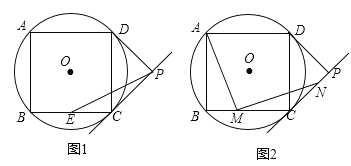
【题目】如图，AD是圆O的切线，切点为A，AB是圆O的弦。过点B作BC//AD，交圆O于点C，连接AC，过点C作CD//AB，交AD于点D。连接AO并延长交BC于点M，交过点C的直线于点P，且BCP=ACD。

（1）判断直线PC与圆O的位置关系，并说明理由：

（2） 若AB=9，BC=6，求PC的长。

Answer 1

【答案】（1）直线PC与圆O相切（2）

【解析】解：（1）直线PC与圆O相切。理由如下：：

如图，连接CO并延长，交圆O于点N，连接BN，

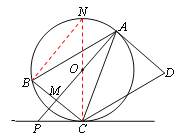
∵AB//CD，∴BAC=ACD。

∵BAC=BNC，∴BNC=ACD。

∵BCP=ACD，∴BNC=BCP。

∵CN是圆O的直径，∴CBN=90。

∴BNCBCN=90，∴BCPBCN=90。

∴PCO=90，即PCOC。

又∵点C在圆O上，∴直线PC与圆O相切。

（2）∵AD是圆O的切线，∴ADOA，即OAD=90。

∵BC//AD，∴OMC=180OAD=90，即OMBC。

∴MC=MB。∴AB=AC。

在Rt△AMC中，AMC=90，AC=AB=9，MC=BC=3，

由勾股定理，得。

设圆O的半径为r，

在Rt△OMC中，OMC=90，OM=AMAO=，MC=3，OC=r，

由勾股定理，得OM 2MC 2=OC 2，即。解得。

在△OMC和△OCP中，∵OMC=OCP，MOC=COP，∴△OMC～△OCP。

∴，即。∴。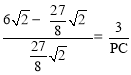

（1）过C点作直径CE，连接EB，由CE为直径得∠E+∠BCE=90°，由AD∥BC得∠ACD=∠BAC，而

∠BAC=∠E，∠BCP=∠ACD，所以∠E=∠BCP，于是∠BCP+∠BCE=90°，然后根据切线的判断得到结论。

（2）根据切线的性质得到OA⊥AD，而BC∥AD，则AM⊥BC，根据垂径定理有BM=CM=BC=3，根据线段垂直平分线的性质有AC=AB=9，在Rt△AMC中根据勾股定理计算出AM= 。设⊙O的半径为r，则OC=r，OM=AM－r=，在Rt△OCM中，根据勾股定理计算出 ，从而由△OMC～△OCP得相似比可计算出PC。