Question

【题目】如图1在△ABC中，D在AB边上，DE⊥BC于E，∠A=2∠BDE.

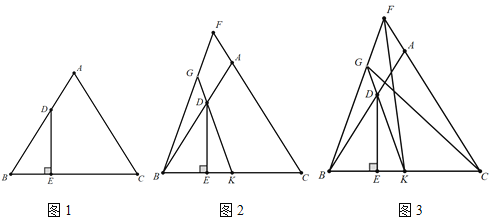
（1）求证：AB=AC；

（2）延长CA至F，连接BF，G在线段BF上，连接DG，∠F=∠BDK，延长GD交BC于K，如图2，试判断线段KG与BG的数量关系，并加以证明；

（3）在（2）的条件下，连接CG、FK，CG=FK，∠CGK=∠BFK，FG=2,CK=3,如图3，求线段BF的长度.

Answer 1

【答案】（1）见解析；（2）KG=BG，证明见解析；（3）BF=6.5.

【解析】

（1）过A作AM⊥BC于M可推DE∥AM可得∠3=∠2，推出∠B=∠C得出结论；

（2）由∠ABC=∠ACB及∠F=∠BDK可得∠GKB=∠GBK，由三角形内角和可得∠BKD=∠FBK可推出BG=GK

（3）延长GK至M使KM=FG=2可证△BFK≌△MGC，可得BK=CM，∠GBK=∠BKG=∠CKM=∠CMK，可得△BGK≌△MCK，所以 ，推出BG=4.5，所以BF=BG+FG=6.5

（1）

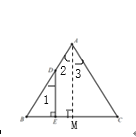
过A作AM⊥BC于M

∵AM⊥BC，DE⊥BC

∴∠DEB=∠AMB=90°，∠AMB=∠AMC=90°

∴DE∥AM

∴∠1=∠2

∵∠BAC=2∠1

∴∠BAC=2∠2

∴∠3=∠2

∴∠B=90°-∠2，∠C=90°-∠3

∴∠B=∠C

∴AB=AC

（2）∵AB=AC

∴∠ABC=∠ACB

∵∠F=∠BDK

∴∠GKB=∠GBK

∵∠DBK+∠BDK+∠BKD=180°

又∵∠BCF+∠F+∠FBK=180°

∴∠BKD=∠FBK

∴BG=GK

（3）

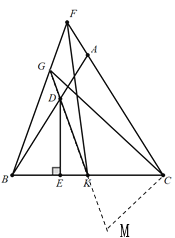
延长GK至M使KM=FG=2

∵BG=GK

∴BG+FG=KM+GK

即BF=MG

又∵∠BFK=∠MGC，FK=GC

∴△BFK≌△MGC

∴∠GBK=∠M，BK=CM

∵∠GBK=∠GKB，∠CKM=∠BKG

∴∠GBK=∠BKG=∠CKM=∠CMK

∴CM=CK=3

∴BK=3

∵∠GBK=∠CMK，∠GKB=∠MKC

∴

∴

∴

∴BG=4.5

∴BF=BG+FG=6.5