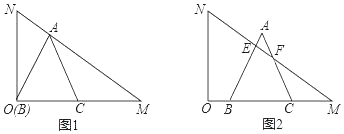��Ŀ����
����Ŀ����һ�麬30���ǵ�ֱ�����ǰ�OMN�����С�MON��90������NMO��30����ON��2![]() �������ֱ�����ǰ尴��ͼ��ʾλ�ðڷţ��ȱ���ABC�Ķ���B���O�غϣ�BC������OM�ϣ���Aǡ������б��MN�ϣ����ȱ���ABC��ͼ1��λ����OM������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���AB��AC�ֱ���б��MN���ڵ�E��F����ͼ2��ʾ��������ABCƽ�Ƶ�ʱ��Ϊt��s����0��t��6����
�������ֱ�����ǰ尴��ͼ��ʾλ�ðڷţ��ȱ���ABC�Ķ���B���O�غϣ�BC������OM�ϣ���Aǡ������б��MN�ϣ����ȱ���ABC��ͼ1��λ����OM������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���AB��AC�ֱ���б��MN���ڵ�E��F����ͼ2��ʾ��������ABCƽ�Ƶ�ʱ��Ϊt��s����0��t��6����
��1���ȱ���ABC�ı߳�Ϊ�� ����
��2�����˶������У����� ��ʱ��MN��ֱƽ��AB��
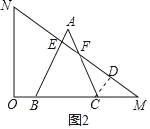
��3����0��t��6ʱ����ֱ�����ǰ�OMN��ȱ���ABC�ص����ֵ����S��ʱ��t֮��ĺ�����ϵʽ��
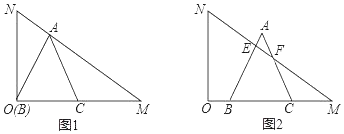
���𰸡���1��3����2��3����3��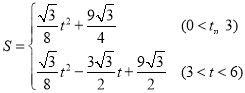 .
.
��������
��1�����ݣ���OMN��30������ABCΪ�ȱ������Σ���֤��OAMΪֱ�������Σ�Ȼ�ɵó��𰸣�
��2����֪����C��M�غ�ʱֱ��MNƽ���߶�AB����ʱOB��3���ɴ˼��ɽ�����⣻
��3�����������ηֱ���⣺��0��t��3ʱ����CD��FM��D������S��S��MEB��2S��MDC�����㼴�ɣ��ڵ�3��t��6ʱ��S��S��MEB��
�⣺��1����Rt��MON�У��ߡ�MON��90����ON��2![]() ����M��30��
����M��30��
��OM��![]() ON��6��
ON��6��
�ߡ�ABCΪ�ȱ�������
���AOC��60����
���OAM��90��
��OA��MN������OAMΪֱ�������Σ�
��OA��![]() OM��
OM��![]() ��6��3��
��6��3��
�ʴ�Ϊ3��
��2����֪����C��M�غ�ʱֱ��MNƽ���߶�AB����ʱOB��3������t��3��
�ʴ�Ϊ3��
��3����֪��OM��6��MN��4![]() ��S��OMN��
��S��OMN��![]() ��2
��2![]() ��6��6
��6��6![]() ��
��
�ߡ�M��30������MBA��60����
���BEM��90����
�ٵ�0��t��3ʱ����CD��FM��D��
�ߡ�ACB��60������M��30������FCB����M+��CFM��
���CFM����M��30����
��CF��CM��
��CD��FM��
��DF��DM��
��S��CMF��2S��CDM��
�ߡ�MEB�ס�MON��
��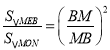 ��
��
��S��MEB��![]() ��
��
�ߡ�MDC�ס�MON��
��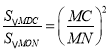 ��
��
��S��MDC��![]() ��
��![]()
��S��S��MEB��2S��MDC����![]() ��
��
�ڵ�3��t��6ʱ��S��S��MEB��![]() ��
��
����������S��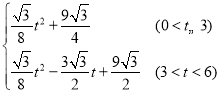 ��
��

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�