题目内容
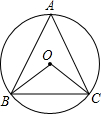
如图,AB是⊙O的直径,点C、D在圆上,且
=
.
(1)求证:AC∥OD.
(2)若∠AOD=110°,求
的度数.

 |
| CD |
 |
| BD |
(1)求证:AC∥OD.
(2)若∠AOD=110°,求
 |
| AC |

(1)证明:如图,连接AD.
∵
=
,
∴
=2
∴∠CAB=2∠DAB.
又∵∠DOB=2∠DAB,
∴∠CAB=∠DOB,
∴AC∥OD;
(2)如图,连接OC.
∵∠AOD=110°,
∴∠DOB=70°.
又∵
=
,
∴∠COD=∠DOB=70°,
∴∠AOC=∠AOD-∠COD=110°-70°=40°,
∴
=40°.

∵
 |
| CD |
 |
| BD |
∴
 |
| BC |
 |
| BD |
∴∠CAB=2∠DAB.
又∵∠DOB=2∠DAB,
∴∠CAB=∠DOB,
∴AC∥OD;
(2)如图,连接OC.
∵∠AOD=110°,
∴∠DOB=70°.
又∵
 |
| CD |
 |
| BD |
∴∠COD=∠DOB=70°,
∴∠AOC=∠AOD-∠COD=110°-70°=40°,
∴
 |
| AC |


练习册系列答案
相关题目