题目内容
【题目】如图,在平面直角坐标系中,![]() ABC,
ABC,![]() A1B1C1,
A1B1C1,![]() A2B2C2,
A2B2C2,![]() A3B3C3…
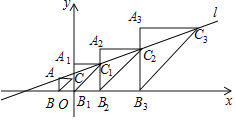
A3B3C3…![]() AnBnCn都是等腰直角三角形,点B,B1,B2,B3…Bn都在x轴上,点B1与原点重合,点A,C1,C2,C3…Cn都在直线l:y=
AnBnCn都是等腰直角三角形,点B,B1,B2,B3…Bn都在x轴上,点B1与原点重合,点A,C1,C2,C3…Cn都在直线l:y=![]() x+
x+![]() 上,点C在y轴上,AB∥A1B1∥A2B2∥…∥AnBn∥y轴,AC∥A1C1∥A2C2∥…∥AnCn∥x轴,若点A的横坐标为﹣1,则点Cn的纵坐标是_____.
上,点C在y轴上,AB∥A1B1∥A2B2∥…∥AnBn∥y轴,AC∥A1C1∥A2C2∥…∥AnCn∥x轴,若点A的横坐标为﹣1,则点Cn的纵坐标是_____.
【答案】![]()
【解析】
分别求出C1,C2,C3,C4,…,探究规律,利用规律解决问题即可.
解:由题意A(﹣1,1),可得C(0,1),
设C1(m,m),则m=![]() m+
m+![]() ,
,
解得m=2,
∴C1(2,2),
设C2(n,n﹣2),则n﹣2=![]() n+
n+![]() ,
,
解得n=5,
∴C2(5,3),
设C3(a,a﹣5),则a﹣5=![]() a+
a+![]() ,
,
解得a=![]() ,
,
∴C3(![]() ,
,![]() ),
),
同法可得C4(![]() ,
,![]() ),…,Cn的纵坐标为
),…,Cn的纵坐标为![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目