Question

已知：如图，EF⊥AB，CD⊥AB，AC⊥BC，∠1=∠2，求证：DG⊥BC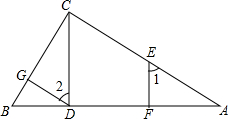

证明：∵EF⊥AB CD⊥AB                  
∴∠EFA=∠CDA=90°（垂直定义）
∠1=∠           
∴EF∥CD                                   
∴∠1=∠2（已知）
∴∠2=∠ACD（等量代换）
∴DG∥AC                      
∴∠DGB=∠ACB                              
∵AC⊥BC（已知）
∴∠ACB=90°（垂直定义）
∴∠DGB=90°即DG⊥BC．

Answer 1

已知，ACD，（两直线平行，同位角相等），（内错角相等，两直线平行），（两直线平行，同位角相等）．

解析试题分析：根据垂直定义求出∠EFA=∠CDA=90°，求出∠1=∠ACD，推出EF∥CD，根据平行线的性质得出∠2=∠ACD，推出DG∥AC，根据平行线的性质推出∠ACB=∠DGB即可．
试题解析：∵EF⊥AB，CD⊥AB（已知），
∴∠EFA=∠CDA=90°（垂直定义），
∴EF∥CD（同位角相等，两直线平行），
∴∠1=∠ACD（两直线平行，同位角相等），
∵∠1=∠2（已知），
∴∠2=∠ACD（等量代换），
∴DG∥AC（内错角相等，两直线平行），
∴∠DGB=∠ACB（两直线平行，同位角相等），
∵AC⊥CB，
∴∠ACB=90°，
∴∠DGB=90°，
即DG⊥BC，
考点：1.平行线的判定与性质；2.垂线．