题目内容
完成证明:(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b
证明:∵a⊥c
∴∠1=________
∵b∥c
∴∠1=∠2 ( )
∴∠2=∠1=90°
∴a⊥b ;
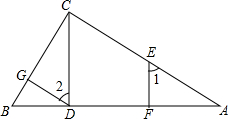
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE
证明:∵AB∥CD (已知)
∴∠B=________( )
∵∠B+∠D="180°" (已知)
∴∠C+∠D="180°" ( )
∴CB∥DE ( )
(1)∠2;两直线平行,同位角相等;等量代换;垂直的定义;
(2)∠C;两直线平行,内错角相等;等量代换;同旁内角互补,两直线平行.
解析试题分析:(1)由垂直得直角,则根据平行线b∥c的性质推知∠2=∠1=90°,即a⊥b;
(2)由平行线的性质、等量代换证得同旁内角∠C+∠D=180°,则易推知CB∥DE.
试题解析:(1)如图1,∵a⊥c(已知),
∴∠1=90°(垂直定义),
∵b∥c(已知),
∴∠1=∠2(两直线平行,同位角相等 ),
∴∠2=∠1=90°(等量代换 ),
∴a⊥b(垂直的定义 );
(2)如图2,∵AB∥CD (已知),
∴∠B=∠C(两直线平行,内错角相等),
∵∠B+∠D=180°(已知),
∴∠C+∠D=180°(等量代换 ),
∴CB∥DE(同旁内角互补,两直线平行).
考点:1.平行线的判定与性质2.垂线.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目


 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是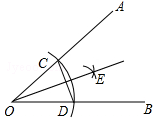
 ;图②中,
;图②中, .图③是该同学所做的一个实验:他将△
.图③是该同学所做的一个实验:他将△ 的直角边
的直角边 与△
与△ 的斜边
的斜边 重合在一起,并将△
重合在一起,并将△ 两点始终在
两点始终在 与点
与点 重合).
重合). 两点间的距离 ;连接
两点间的距离 ;连接 的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”) 与
与 度数之和是否为定值,请加以说明;
度数之和是否为定值,请加以说明; 平行?如果能,请求出此时
平行?如果能,请求出此时

