题目内容
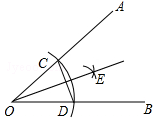
如图,已知AB∥CD,∠AEC=90°,那么∠A与∠C的度数和为多少度?为什么?
解:∠A与∠C的度数和为 _________ .
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°( _________ ).
∵AB∥CD( _________ ),EF∥AB,
∴EF∥CD( _________ )
∴ _________ (两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= _________ °(等式的性质)
即∠A+∠AEC+∠C= _________ °
∵∠AEC=90°(已知)
∴∠A+∠C= _________ °(等式的性质).
270°,完成理由证明见解析.
解析试题分析:
关键是过点E作EF∥AB,
则利用两直线平行,同旁内角互补。得∠A+∠AEF=180°
再有AB∥CD和 EF∥AB,可知EF∥CD
由两直线平行,同旁内角互补,得到∠C+∠CEF=180°
则得到∠A+∠AEF+∠CEF+∠C=360°,据等式的性质 即∠A+∠AEC+∠C=360°
又∠AEC=90°得到∠A+∠C=270°.
试题解析:∠A与∠C的度数和为 270°.
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°(两直线平行,同旁内角互补).
∵AB∥CD( 已知 ),EF∥AB,
∴EF∥CD(平行于同一条直线的两条直线互相平行)
∴∠C+∠CEF=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= 360°(等式的性质)
即∠A+∠AEC+∠C= 360°°
∵∠AEC=90°(已知)
∴∠A+∠C= 270°(等式的性质).
考点:两直线平行,同旁内角互补.

练习册系列答案
相关题目
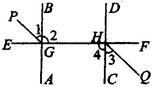




 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是