题目内容
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度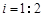 且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
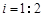 且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)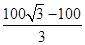
过点P作PF⊥OC,垂足为F.
在Rt△OAC中,由∠OAC=60°,OA=100,得OC=OA tan∠OAC=100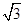 米.
米.
过点P作PE⊥AB,垂足为E.由i=1:2,设PE=x,则AE=2x.
∴PF=OE=100+2x,CF=100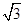 –x.
–x.
在Rt△PCF中,由∠CPF=45°,∴PF=CF,即100+2x=100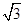 –x,
–x,
∴x=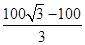 ,
,
即PE=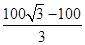 ……10分
……10分
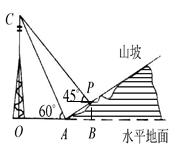
在图中共有三个直角三角形,即RT△AOC、RT△PCF、RT△PAE,利用60°、45°以及坡度比,分别求出CO、CF、PE,然后根据三者之间的关系,列方程求解即可解决.
在Rt△OAC中,由∠OAC=60°,OA=100,得OC=OA tan∠OAC=100
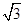 米.
米.过点P作PE⊥AB,垂足为E.由i=1:2,设PE=x,则AE=2x.
∴PF=OE=100+2x,CF=100
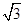 –x.
–x.在Rt△PCF中,由∠CPF=45°,∴PF=CF,即100+2x=100
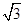 –x,
–x, ∴x=
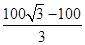 ,
,即PE=
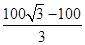 ……10分
……10分
在图中共有三个直角三角形,即RT△AOC、RT△PCF、RT△PAE,利用60°、45°以及坡度比,分别求出CO、CF、PE,然后根据三者之间的关系,列方程求解即可解决.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
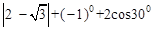
 交AC于点E,F是
交AC于点E,F是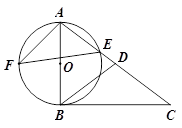
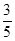 ,AE=
,AE=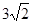 ,求sin∠AFE的值和AF的长.
,求sin∠AFE的值和AF的长.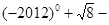 4sin
4sin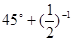

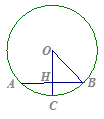
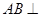 半径
半径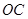 于
于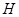 ,
,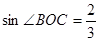 ,则
,则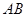 的长度为
的长度为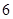
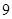
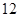
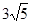
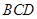 中,∠
中,∠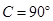 ,∠
,∠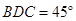 ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出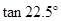 的值吗?
的值吗?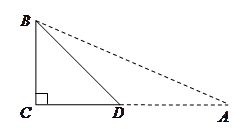
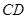 到点
到点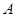 ,使
,使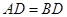 ,连结
,连结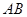 .
.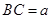 (
(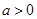 ).
). .
.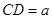 ,
,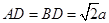 .
.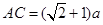 .
.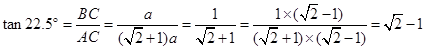 .
.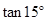 的值;
的值;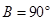 ,∠
,∠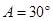 ,
,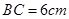 ;图2中,∠
;图2中,∠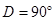 ,∠
,∠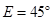 ,
,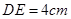 .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△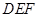 的直角边
的直角边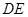 与△
与△ 的斜边
的斜边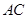 重合在一起,并将△
重合在一起,并将△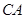 方向移动.在移动过程中,
方向移动.在移动过程中,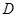 、
、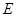 两点始终在
两点始终在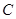 重合).
重合).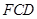 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”)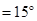 ?如果存在,求出
?如果存在,求出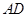 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.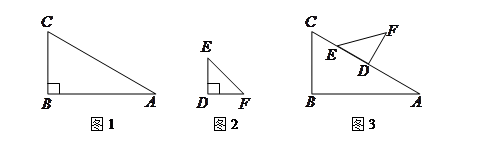
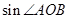 = .
= .
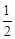 ,AE=7,求DE。
,AE=7,求DE。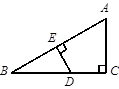
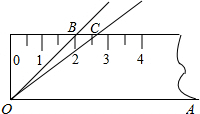
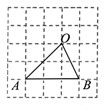
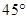 的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将
的∠AOB按图摆放在一把刻度尺上,顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2cm,若按相同的方式将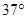 的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm
的∠AOC放置在该尺上,则OC与尺上沿的交点C在尺上的读数约为 ▲ cm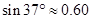 ,
,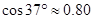 ,
,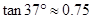 )
)