题目内容
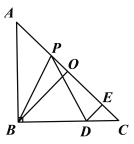
【题目】如图,在△ABC中,AC=AB,把△ABC绕点A顺时针旋转得到△ADE(点B、C分别对应点D、E),BD和CE交于点F.
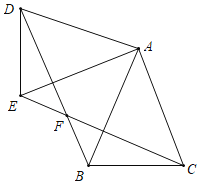
(1)求证:CE=BD;
(2)若AB=2,∠BAC=45°,当四边形ADFC是平行四边形时,求BF的长.
【答案】(1)见解析;(2)2![]() ﹣2
﹣2
【解析】
(1)由于旋转,得到△ABC≌△ADE ,由全等性质去证明∠DAB=∠EAC,便可证明△AEC≌△ADB,从而得到结论.
(2)由四边形ADFC是平行四边形,得到DF=AC,AC∥BD,再根据∠BAD=90°,得到BD=![]() AB=2
AB=2![]() ,最后得到BF=BD﹣DF计算出值.
,最后得到BF=BD﹣DF计算出值.
证明:(1)∵把△ABC绕点A顺时针旋转得到△ADE
∴△ABC≌△ADE
∴AD=AB,AE=AC,∠DAE=∠BAC
∴∠DAE+∠BAE=∠BAC+∠BAE
∴∠DAB=∠EAC,
∵AB=AC
∴AD=AB=AC=AE
∵∠DAB=∠EAC,AD=AB,AC=AE
∴△AEC≌△ADB(SAS)
∴CE=BD
(2)∵四边形ADFC是平行四边形
∴DF=AC,AC∥BD
∴∠ABD=∠BAC=45°
∵AB=AD
∴∠DBA=∠BDA=45°
∴∠BAD=90°
∴BD=![]() AB=2
AB=2![]()
∵DF=AC=AB=2
∴BF=BD﹣DF=2![]() ﹣2
﹣2

练习册系列答案
相关题目