题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.
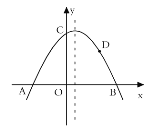
(1)求抛物线的表达式;
(2)点![]() 是抛物线上一点.
是抛物线上一点.
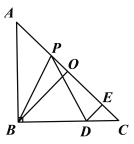
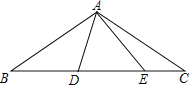
①在抛物线的对称轴上,求作一点![]() ,使得
,使得![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标;
的坐标;
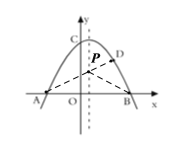
②连接![]() 并延长,过抛物线上一点
并延长,过抛物线上一点![]() (点
(点![]() 不与点
不与点![]() 重合)作
重合)作![]() 轴,垂足为
轴,垂足为![]() ,与射线
,与射线![]() 交于点
交于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①连接
;(2)①连接![]() 交抛物线对称轴于点
交抛物线对称轴于点![]() ,则点
,则点![]() 即为所求,点
即为所求,点![]() 的坐标为
的坐标为![]() ;②存在;点
;②存在;点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)由![]() ,
,![]() 得到A(-2,0),C(3,0),即可写出抛物线的交点式.
得到A(-2,0),C(3,0),即可写出抛物线的交点式.
(2)①因为![]() 关于对称轴对称,所以
关于对称轴对称,所以![]() ,由两点之间线段最短,知连接
,由两点之间线段最短,知连接![]() 交抛物线对称轴于点
交抛物线对称轴于点![]() ,则点
,则点![]() 即为所求,先用待定系数法求出
即为所求,先用待定系数法求出![]() 解析式,将对称轴代入得到
解析式,将对称轴代入得到![]() 点坐标.
点坐标.
②设点![]() ,根据抛物线的解析式、直线
,根据抛物线的解析式、直线![]() 的解析式,写出Q、M的坐标,分当
的解析式,写出Q、M的坐标,分当![]() 在
在![]() 上方、下方两种情况,列关于m的方程,解出并取大于-2的解,即可写出
上方、下方两种情况,列关于m的方程,解出并取大于-2的解,即可写出![]() 的坐标.
的坐标.
(1)∵![]() ,
,![]() ,
,
结合图象,得A(-2,0),C(3,0),
∴抛物线![]() 可表示为:
可表示为:![]() ,
,
∴抛物线的表达式为![]() ;
;
(2)①∵![]() 关于对称轴对称,
关于对称轴对称,
∴![]() ,
,
∴连接![]() 交抛物线对称轴于点
交抛物线对称轴于点![]() ,则点
,则点![]() 即为所求.
即为所求.
将点![]() ,
,![]() 的坐标代入一次函数表达式
的坐标代入一次函数表达式![]() ,
,
得直线![]() 的函数表达式为
的函数表达式为![]() .
.
抛物线的对称轴为直线![]() ,
,
当![]() 时,
时,![]() ,
,
故点![]() 的坐标为
的坐标为![]() ;
;
②存在;设点![]() ,则
,则![]() ,
,![]() .
.
当![]() 在
在![]() 上方时,
上方时,
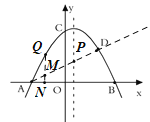
![]() ,
,![]() ,
,![]() ,解得
,解得![]() (舍)或
(舍)或![]() ;
;
当![]() 在
在![]() 下方时,
下方时,
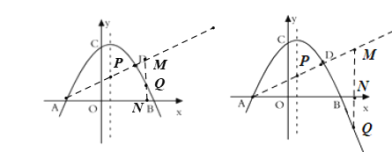
![]() ,
,![]() ,
,![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
综上所述,![]() 的值为
的值为![]() 或5,
或5,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目