题目内容
【题目】Rt△ABC 中,∠BAC=90°,AB=AC=2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.
【答案】4或![]() 或
或![]()
【解析】
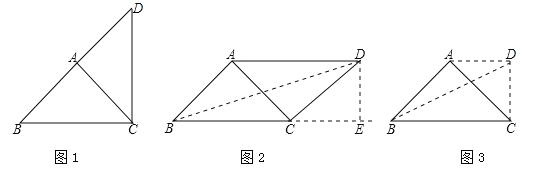
分三种情况讨论:①以A为直角顶点,向外作等腰直角三角形DAC;②以C为直角顶点,向外作等腰直角三角形ACD;③以AC为斜边,向外作等腰直角三角形ADC.分别画图,并求出BD.
①以A为直角顶点,向外作等腰直角三角形DAC,如图1.
∵∠DAC=90°,且AD=AC,
∴BD=BA+AD=2+2=4;
②以C为直角顶点,向外作等腰直角三角形ACD,如图2.
连接BD,过点D作DE⊥BC,交BC的延长线于E.
∵△ABC是等腰直角三角形,∠ACD=90°,
∴∠DCE=45°.
又∵DE⊥CE,
∴∠DEC=90°,
∴∠CDE=45°,
∴CE=DE=2![]() .
.
在Rt△BAC中,BC![]()
![]() ,∴BD
,∴BD![]()
![]() ;
;
③以AC为斜边,向外作等腰直角三角形ADC,如图3.
∵∠ADC=90°,AD=DC,且AC=2,
∴AD=DC=ACsin45°=2![]() .
.
又∵△ABC、△ADC是等腰直角三角形,
∴∠ACB=∠ACD=45°,
∴∠BCD=90°.
又∵在Rt△ABC中,BC![]()
![]() ,
,
∴BD![]() .
.
故BD的长等于4或![]() 或
或![]() .
.
故答案为4或![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




