题目内容
【题目】平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,且
,且![]() 满足
满足![]() ;
;
(1)矩形的顶点![]() 的坐标是( , ).
的坐标是( , ).
(2)若![]() 是
是![]() 中点,沿
中点,沿![]() 折叠矩形
折叠矩形![]() 使
使![]() 点落在
点落在![]() 处,折痕为
处,折痕为![]() ,连
,连![]() 并延长交
并延长交![]() 于
于![]() ,求直线
,求直线![]() 的解析式.
的解析式.
(3)将(2)中直线![]() 向左平移
向左平移![]() 个单位交
个单位交![]() 轴于
轴于![]() ,
,![]() 为第二象限内的一个动点,且
为第二象限内的一个动点,且![]() ,求
,求![]() 的最大值.
的最大值.

【答案】(1)(6,8);(2)![]() ;(3)
;(3)![]()
【解析】
(1)将![]() 整理即为
整理即为![]() ,根据平方和二次根式的性质可得:
,根据平方和二次根式的性质可得:![]() ,
,![]() ,求解即可得到a、b的值,即可求出B点坐标;
,求解即可得到a、b的值,即可求出B点坐标;
(2)作辅助线过点E作x轴的平行线交y轴于点G、交AB于点H,先证明![]() ,设:
,设:![]() ,
,![]() ,得
,得![]() ,即:
,即:![]() ,
,
解出m、n的值,即求出E点坐标,将点C、E的坐标代入一次函数表达式求解即可;
(3)过点N、O、M作圆R(R为圆心),连接RM、RO,当F、R、N三点共线时,FN最大,即可求解.
(1)将![]() 整理即为
整理即为![]() ,
,
∵根据平方和二次根式的性质可得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
∴B点坐标为:(6,8);
(2)如图过点E作x轴的平行线交y轴于点G、交AB于点H,
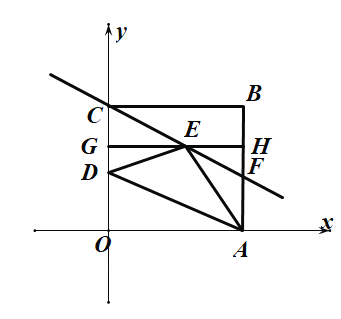
设:![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
解得:![]() ,
,![]() ,
,
∴E点坐标为![]() ,
,
设直线CE的解析式为:![]() ,将点C、E的坐标代入一次函数表达式并解得:
,将点C、E的坐标代入一次函数表达式并解得:
直线CE的表达式为:![]() ;
;
(3) ![]() 中,当x=6时,y=4,故点F(6,4),
中,当x=6时,y=4,故点F(6,4),
直线CE向左平移一个单位后的表达式为:![]() ,可求出M点坐标为:
,可求出M点坐标为:![]() ,
,
如图过点N、O、M作圆R(R为圆心),连接RM、RO,

当F、R、N三点共线时,FN最大,
∵![]() ,
,
∴![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
∴点R的坐标为![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴由点F、R的坐标得, ![]() ,
,
FN的最大值=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






