Question

【题目】如图所示，∠MON=45°，点P是∠MON内一点，过点P作PA⊥OM于点A、PB⊥ON于点B，且PB=2 ．取OP的中点C，联结AC并延长，交OB于点D．

（1）求证：∠ADB=∠OPB；
（2）设PA=x，OD=y，求y关于x的函数解析式；
（3）分别联结AB、BC，当△ABD与△CPB相似时，求PA的长．

Answer 1

【答案】
（1）

证明：如图，∵PA⊥OM，CO=CP，

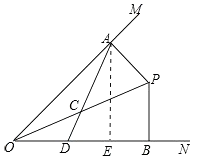
∴CO=CP=CA，

∴∠CAO=∠COA，

过A作AE⊥OB于E，

∵∠MON=45°，

∴∠AOE=∠OAE=45°，

∴∠POB=∠DAE，

∵PB⊥OB，

∴∠ADB=∠OPB

（2）

解：如图1，

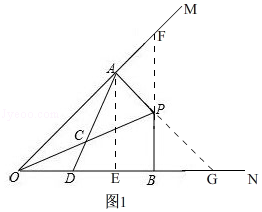
延长BP交OM于F，

∵BP⊥ON，PA⊥OM，

∴∠OBP=∠OAP=90°，

∵∠MON=45°，

∴∠AFB=45°，

在Rt△APF中，AP=x，∠OFB=45°，

∴PF= x，

∴BF=PF+PB= x+2 = （x+2），

在Rt△OBF中，OB=BF= （x+2）

延长AP交ON于G，

同理：PG= PB=4，

∴OA=AG=AP+PG=x+4，

过点A作AE⊥ON，

∴OE=AE= OA= （x+4），

∴DE=OE﹣OD= （x+4）﹣y

由（1）知，∠ADE=∠OPB，

∵∠AED=∠OBP=90°，

∴△ADE∽△OPB，

∴ ，

∴ ，

∴y=

（3）

解：如图2，

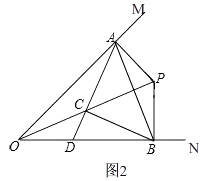
在Rt△OAP中，点C是OP中点，

∴AC=OC= OP，

在Rt△OBP中，点C是OP中点，

∴BC=OC= OP，

∴AC=BC，

∵AC=OC，

∴∠ACP=2∠AOP，

∵OC=BC，

∴∠BCP=2∠BOP，

∴∠ACB=∠ACP+∠BCP=2（∠AOP+∠BOP）=2∠AOB=90°，

∴∠BAC=∠CAB=45°，

∵∠OBP=90°，

∴∠OBC+∠ABP=45°

∵当△ABD与△CPB相似时，

∵∠ADB=∠CPB，

∴∠ABD=∠PBC，

∴∠OBC=∠ABP= ×45°=22.5°，

∵OC=BC，

∴∠BOC=∠OBC=22.5°，

∴∠AOP=∠BOP，

∴OP是∠MON的角平分线，

∵PA⊥OM，PB⊥ON，

∴PA=PB=2

【解析】（1）先判断出∠DAE=∠POB，再利用等角的余角相等即可得出结论；（2）先利用等腰直角三角形的性质得出OB=BF= （x+2），同理得出OA=x+4，即可得出AE，OE，进而得出DE，最后用△ADE∽△OPB的比例式建立方程化简即可得出结论；（3）先利用直角三角形斜边的中线等于斜边的一半和三角形外角的性质判断出△ABC是等腰直角三角形，即可得出∠OBC+∠ABP=45°，再用△ABD与△CPB得出，∠ABD=∠PBC，即∠OBC=∠ABP= ×45°=22.5°，进而得出OP是∠MON的平分线即可得出结论．
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°，以及对直角三角形斜边上的中线的理解，了解直角三角形斜边上的中线等于斜边的一半．