ЬтФПФкШн
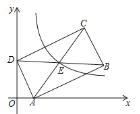
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cОЙ§ЕуB(4ЃЌ0)ЃЌC(0ЃЌЉ2)ЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЌгыxжсЕФСэвЛИіНЛЕуЮЊЕуAЃЎ
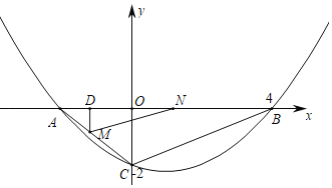
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуMДгЕуAГіЗЂЃЌбиACЯђЕуCдЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЭЌЪБЕуNДгЕуBГіЗЂЃЌбиBAЯђЕуAдЫЖЏЃЌЫйЖШЮЊ2ИіЕЅЮЛГЄЖШ/УыЃЌЕБЕуMЁЂNгавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЌСЌНгMNЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЕБtЮЊКЮжЕЪБЃЌAMNЕФУцЛ§SзюДѓЃЌВЂЧѓГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуPдкxжсЩЯЃЌЕуQдкХзЮяЯпЩЯЃЌЪЧЗёДцдкЕуPЁЂQЃЌЪЙЕУвдЕуPЁЂQЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌSзюДѓжЕЮЊ
ЪБЃЌSзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉДцдкЃЌP1(Љ3+
ЃЛЃЈ3ЃЉДцдкЃЌP1(Љ3+![]() ЃЌ0)ЃЌP2(Љ3Љ
ЃЌ0)ЃЌP2(Љ3Љ![]() ЃЌ0)ЃЌP3(6ЃЌ0)ЃЌP4(2ЃЌ0)
ЃЌ0)ЃЌP3(6ЃЌ0)ЃЌP4(2ЃЌ0)
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈШЗЖЈКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉгЩХзЮяЯпЕФЖдГЦаджЪЧѓЕУAЃЈ-2ЃЌ0ЃЉЃЌдђAB=6ЃЛЕБЕуNдЫЖЏtУыЪБЃЌBN=2tЃЌдђAN=6-2tЃЌЙ§ЕуMзїMDЁЭxжсгкЕуDЃЌЙЙдьжБНЧШ§НЧаЮЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНСаГіКЏЪ§ЙиЯЕЪНЃЌРћгУХфЗНЗЈЧѓЕУзюДѓжЕЃЛ
ЃЈ3ЃЉашвЊЗжШ§жжЧщПіЬжТлЃЌгУЦНвЦЕФжЊЪЖЯШЧѓГіЕуQЕФКсзјБъЃЌШЛКѓЭЦГіЕуPЕФзјБъЃЎ
ЃЈ1ЃЉвРЬтвтЃЌНЋBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ2ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН1ЃЌДњШыХзЮяЯпНтЮіЪНЃЌ
ЕУ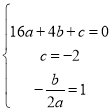 ЃЌ
ЃЌ
НтЕУЃК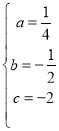 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпЖдГЦжсЮЊжБЯпxЃН1ЃЌBЃЈ4ЃЌ0ЃЉЃЎ
ЁрAЃЈЉ2ЃЌ0ЃЉЃЌдђABЃН6ЃЌ
ЕБЕуNдЫЖЏtУыЪБЃЌBNЃН2tЃЌдђANЃН6Љ2tЃЌ
ШчЭМ1ЃЌЙ§ЕуMзїMDЁЭxжсгкЕуDЃЎ
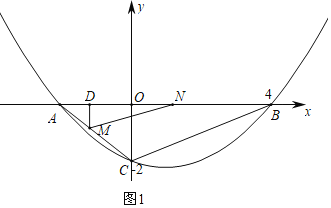
ЁпOAЃНOCЃН2ЃЌ
ЁрЁїOACЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯOACЃН45ЁуЃЎ
гжЁпDMЁЭOAЃЌ
ЁрЁїDAMЪЧЕШбќжБНЧШ§НЧаЮЃЌADЃНDMЃЌ
ЕБЕуMдЫЖЏtУыЪБЃЌAMЃНtЃЌ
ЁрMD2+AD2ЃНAM2ЃНt2ЃЌ
ЁрDMЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁргЩЖўДЮКЏЪ§ЕФЭМЯѓМАаджЪПЩжЊЃЌЕБ![]() ЪБЃЌSзюДѓжЕЮЊ
ЪБЃЌSзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкЃЌРэгЩШчЯТЃК
ЂйЕБЫФБпаЮCBQPЮЊЦНааЫФБпаЮЪБЃЌCBгыPQЦНааЧвЯрЕШЃЌ
ЁпBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ2ЃЉЃЌ
ЁрyBЉyCЃНyQЉyPЃН2ЃЌxBЉxCЃНxQЉxPЃН4ЃЌ
ЁпyPЃН0ЃЌ
ЁрyQЃН2ЃЌ
НЋyЃН2ДњШы![]() ЃЌ
ЃЌ
ЕУ x1ЃН![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЌ
ЃЌ
ЁрЕБxQЃН![]() ЪБЃЌxPЃН
ЪБЃЌxPЃН![]() ЃЛЕБxQЃН
ЃЛЕБxQЃН![]() ЪБЃЌxPЃН
ЪБЃЌxPЃН![]() ЃЌ
ЃЌ
ЁрP1ЃЈ![]() ЃЌ0ЃЉЃЌP2ЃЈ
ЃЌ0ЃЉЃЌP2ЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂкЕБЫФБпаЮCQPBЮЊЦНааЫФБпаЮЪБЃЌBPгыCQЦНааЧвЯрЕШЃЌ
ЁпyPЃНyBЃН0ЃЌ
ЁрyQЃНyCЃНЉ2ЃЌ
НЋyЃНЉ2ДњШы![]() ЃЌ
ЃЌ
ЕУ x1ЃН0ЃЈЩсШЅЃЉЃЌx2ЃН2ЃЌ
ЁрxQЃН2ЪБЃЌ
ЁрxPЉxBЃНxQЉxCЃН2ЃЌ
ЁрxPЃН6ЃЌ
ЁрP3ЃЈ6ЃЌ0ЃЉЃЛ
ЂлЕБЫФБпаЮCQBPЮЊЦНааЫФБпаЮЪБЃЌBPгыCQЦНааЧвЯрЕШЃЌ
гЩЂкжЊЃЌxQЃН2ЃЌ
ЁрxBЉxPЃНxQЉxCЃН2ЃЌ
ЁрxPЃН2ЃЌ
ЁрP4ЃЈ2ЃЌ0ЃЉЃЛ
злЩЯЫљЪіЃЌДцдкТњзуЬѕМўЕФЕуPга4ИіЃЌЗжБ№ЪЧP1ЃЈЉ3+![]() ЃЌ0ЃЉЃЌP2ЃЈЉ3Љ
ЃЌ0ЃЉЃЌP2ЃЈЉ3Љ![]() ЃЌ0ЃЉЃЌP3ЃЈ6ЃЌ0ЃЉЃЌP4ЃЈ2ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЌP3ЃЈ6ЃЌ0ЃЉЃЌP4ЃЈ2ЃЌ0ЃЉЃЎ