��Ŀ����
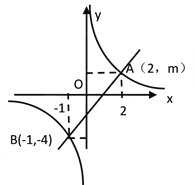
����Ŀ����ƽ��ֱ������ϵ�У���֪��A��a��0����B��b��3����C��4��0����������![]() +��a��b+6��2��0���߶�AB��y���ڵ�F����D��y���������ϵ�һ�㣮
+��a��b+6��2��0���߶�AB��y���ڵ�F����D��y���������ϵ�һ�㣮
��1�������A��B�����ꣻ
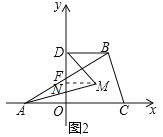
��2����ͼ2����DB��AC����BAC��a����AM��DM�ֱ�ƽ�֡�CAB����ODB�����AMD�Ķ��������ú�a�Ĵ���ʽ��ʾ����
��3����ͼ3�����������Ƿ����һ��P��ʹ�á�ABP������͡�ABC�������ȣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��A����3��0����B��3��3������2����AMD��45��+![]() a����3������.
a����3������.
��������
��1�����ݷǸ��������ʵõ�����a��b�Ķ�Ԫһ�η����飬Ȼ����⼴�ɣ�
��2������M��MN��DB����y���ڵ�N������ƽ���ߵ�������֤��AMD����AMN+��DMN���ٸ��ݽ�ƽ���ߵĶ����������ɵý⣻
��3�����ڣ���F��0��t��������S��AOF+S��BOF��S��AOB�����F�����꣬�ٷ�P����y���ϣ���x������������������ۼ���.
�⣺��1����![]() +��a��b+6��2��0��
+��a��b+6��2��0��
��a+b��0��a��b+6��0��
��a����3��b��3��
��A����3��0����B��3��3����
��2����ͼ2������M��MN��DB����y���ڵ�N��
���DMN����BDM��
����DB��AC��
��MN��AC��
���AMN����MAC��
��DB��AC����DOC��90����
���BDO��90����
����AM��DM�ֱ�ƽ����CAB����ODB����BAC��a��
���MAC��![]() a����BDM��45����
a����BDM��45����
���AMN��![]() a����DMN��45����
a����DMN��45����
���AMD����AMN+��DMN��45��+![]() a��
a��
��3�����ڣ�
����OB����ͼ3��

��F��0��t����
��S��AOF+S��BOF��S��AOB��
��![]() 3t+
3t+![]() t3��
t3��![]() ��3��3�����t��
��3��3�����t��![]() ��
��
��F��������0��![]() ����
����
��ABC�������![]() ��7��3��
��7��3��![]() ��
��
��P����y����ʱ����P��0��y����
��S��ABP��S��APF+S��BPF��
��![]() |y��
|y��![]() |3+
|3+![]() |y��
|y��![]() |3��
|3��![]() ��
��
���y��5��y����2��
����ʱP������Ϊ��0��5����0����2����
��P����x����ʱ����P��x��0����
��![]() |x+3|3��
|x+3|3��![]() ��
��
���x����10��x��4��
����ʱP������Ϊ����10��0����
���Ͽ�֪�������������ĵ�P��������Ϊ��0��5����0����2����10��0����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�