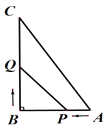Question

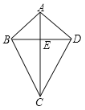
【题目】如图，菱形ABCD中，E为对角线BD的延长线上一点．

（1）求证：AE=CE．

（2）若BC=6，AE=10，∠BAE=120，求BE的长，并直接写出DE的长为 ．

Answer 1

【答案】（1）见解析；（2）BE=11，.

【解析】

（1）由菱形的性质得出AB=CB，∠ABE=∠CBE，证明△ABE≌△CBE，即可得出结论；

（2）连接AC交BD于O，作EF⊥BA延长线于点F，先求AF，EF的长度，再根据勾股定理求出BE长，证明△AOB∽△EFB，从而求出BO长，即可求出DE的长度.

解：（1）∵四边形ABCD是菱形，

∴AB=CB，∠ABE=∠CBE，

在△ABE和△CBE中

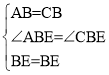
∴△ABE≌△CBE（SAS），

∴AE=CE；

（2）连接AC交BD于O，作EF⊥BA延长线于点F，如图所示：

∵∠BAE=120°，

∴∠EAF=180°-∠BAE=60°，

∴∠AEF=90°-60°=30°，

∵AE=10，

∴AF=，

∴，

∵BC=6，

∴BA=BC=6，

∴BF=11，

∴，

∵四边形ABCD为菱形，

∴AC⊥BD,

∴△AOB∽△EFB，

∴，即，

∴，

∴，

∴.