题目内容
【题目】如图,在平面直角坐标系中,半径为1的圆从原点出发沿x轴正方向滚动一周,圆上一点由原点O到达点O′,圆心也从点A到达点A′.
(1)点O′的坐标为 ,点A′的坐标为 ;
(2)若点P是圆在滚动过程中圆心经过的某一位置,求以点P,点O,点O′为顶点的三角形的面积.
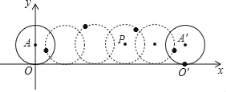
【答案】(1)(2π,0)、(2π,1);(2)S△POO′=π.
【解析】
(1)由半径为1的圆从原点出发沿x轴正方向滚动一周,
得到OO′=AA′=2π,则可求出点O′和点A′;
(2)由(1)可得O'O的长度,且P到O'O的距离始终是1,根据三角形的面积公式即可得到答案.
(1)∵半径为1的圆从原点出发沿x轴正方向滚动一周,
∴⊙O滚动的距离OO′=AA′=2π,
则点O′的坐标为(2π,0),点A′的坐标为(2π,1),
故答案为:(2π,0)、(2π,1);
(2)S△POO′=![]() ×2π×1=π.
×2π×1=π.

练习册系列答案
相关题目