题目内容
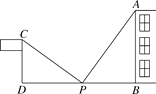
【题目】.已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;

(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() .
.![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
【答案】(1)详见解析;(2)![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 矩形
矩形![]() 面积的
面积的![]() .
.
【解析】
(1)结合矩形的性质和已知条件可证![]() ,根据全等三角形对应边相等即知
,根据全等三角形对应边相等即知![]() ,此题得证;(2)可利用直角三角形中
,此题得证;(2)可利用直角三角形中![]() 角所对的直角边等于斜边的一半确定三角形的面积与矩形的面积之间的等量关系..
角所对的直角边等于斜边的一半确定三角形的面积与矩形的面积之间的等量关系..
(1)证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,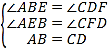 ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 的面积
的面积![]() 矩形
矩形![]() 面积的
面积的![]() .
.
理由如下:
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的面积
的面积![]() 矩形
矩形![]() 的面积,
的面积,
∵![]() ,
,
∴![]() 的面积
的面积![]() 矩形
矩形![]() 的面积;
的面积;
作![]() 于
于![]() ,如图所示:
,如图所示:
∵![]() ,
,
∴![]() ,
,
∴![]() 的面积
的面积![]() 矩形
矩形![]() 的面积,
的面积,
同理:![]() 的面积
的面积![]() 矩形
矩形![]() 的面积.
的面积.


【题目】核桃和枣是我省著名的农特产,它们营养丰富,有益人体健康,深受老百姓喜爱。某超市从农贸批发市场批发核桃和枣进行零售,批发价和零售价格如下表所示:
名称 | 核桃 | 枣 |
批发价(元/ | 12 | 9 |
零售价(元/ | 18 | 12 |
请解答下列问题.
(1)第一天,该超市从批发市场批发核桃和枣共350![]() ,用去了3600元钱,求当天核桃和枣各批发多少kg?
,用去了3600元钱,求当天核桃和枣各批发多少kg?
(2)第二天,该超市用3600元钱仍然批发核桃和枣(批发价和零售价不变),要想将第二天批发的核桃和枣全部售完后,所获利润不低于40%,则该超市第二天至少批发核桃多少kg?
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?