��Ŀ����
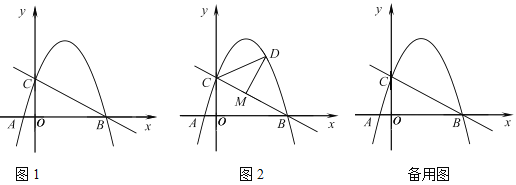
����Ŀ��һ���쳵�Ӽؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ��������쳵���ҵصľ���Ϊy1��km�����������ҵصľ���Ϊy2��km����������ʻʱ��Ϊx��h��������֮��ľ���Ϊs��km����y1��y2��x�ĺ�����ϵͼ����ͼ1��ʾ��s��x�ĺ�����ϵͼ����ͼ2��ʾ���������жϣ���ͼ1��a��3���ڵ�x��![]() hʱ�������������۵�x��
hʱ�������������۵�x��![]() ʱ���������60km����ͼ2��C������Ϊ��3��180�����ݵ�x��
ʱ���������60km����ͼ2��C������Ϊ��3��180�����ݵ�x��![]() h��
h��![]() hʱ���������200km��������ȷ����_____����д��������ȷ�жϵ���ţ�
hʱ���������200km��������ȷ����_____����д��������ȷ�жϵ���ţ�

���𰸡��٢ڢܣ�
��������
����S��x֮��ĺ�����ϵʽ���Եõ���λ��C��ʱ������֮��ľ������ӱ仺����ʱ�쳵��վ����ʱa=3���ʢ���ȷ������������֪y1=y2���з������ɵ�x��ֵΪ![]() ���ʢ���ȷ��������������ǣ�����ǰ���������������60km��x��
���ʢ���ȷ��������������ǣ�����ǰ���������������60km��x��![]() ������ǰ��ʱ�䣬�ʢ���ȷ����ȷ��b��ֵ�����ݺ�����ͼ����Եõ�C�ĵ�����꣬�ʢ���ȷ������������ǰ����������������������ۣ��������x��ֵ����x=
������ǰ��ʱ�䣬�ʢ���ȷ����ȷ��b��ֵ�����ݺ�����ͼ����Եõ�C�ĵ�����꣬�ʢ���ȷ������������ǰ����������������������ۣ��������x��ֵ����x=![]() hʱ�������⣬�ʢݲ���ȷ��
hʱ�������⣬�ʢݲ���ȷ��
�⣺����S��x֮��ĺ�����ͼ���֪����λ��C��ʱ������֮��ľ������ӱ仺��
���ɴ˿��Եõ�a��3���ʢ���ȷ��
��y1��kx+b������0��300������3��0�����룬
�ã�![]() ����ã�
����ã�![]() ��
��
��y1����100x+300��
��y2��mx��
���㣨5��300�����룬�ã�5m��300��
��ã�m��60��
���������ҵصľ���y2����ʽΪ��y2��60x��
�൱y1��y2ʱ������������
�ɵã���100x+300��60x��
��ã�x��![]() h���ʢ���ȷ��
h���ʢ���ȷ��
������������ǣ�����ǰ�������60km��
��100x+300��60x��60����ã�x=![]() h��
h��
�������������60km��
60x������100x+300����60����ã�x=![]() h��
h��
�൱x��![]() h��
h��![]() hʱ���������60km���ʢ۲���ȷ��
hʱ���������60km���ʢ۲���ȷ��
�쳵ÿСʱ��ʻ![]() ��100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ300ǧ�ף�
��100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ300ǧ�ף�
��b��300����100+60����![]() ��
��
�ɺ�����ͼ����Եõ�C�ĵ�ĺ�����Ϊ3�����쳵�����ҵأ���ʱ�������ߵ�·��Ϊ3��60��180ǧ�ף�
��C������Ϊ��3��180�����ʢ���ȷ��
������������ǣ�����ǰ�������200km��
��100x+300��60x��200����ã�x=![]() h��
h��
�������������60km��
60x������100x+300����200����ã�x=![]() h��
h��
��![]() >3��
>3��
�൱x=![]() h�������⣬��ȥ��
h�������⣬��ȥ��
�൱x��![]() hʱ���������200km���ʢݲ���ȷ��
hʱ���������200km���ʢݲ���ȷ��
�ʴ�Ϊ���٢ڢܣ�