题目内容
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
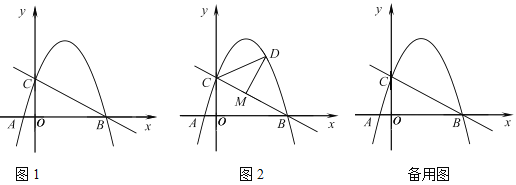
(1)求抛物线的解析式;
(2)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
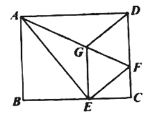
,使得![]() 是等腰三角形,请求出点
是等腰三角形,请求出点![]() 的坐标;
的坐标;
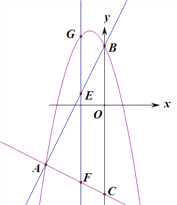
(3)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一个动点.过点
上方抛物线上的一个动点.过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,请求出点
的2倍?若存在,请求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() 、
、![]() (3)2或
(3)2或![]()
【解析】
(1)把点![]() ,
,![]() 代入抛物线
代入抛物线![]() ,即可求出抛物线的解析式;
,即可求出抛物线的解析式;
(2)求出点C的坐标,求出![]() 的长度,分①当
的长度,分①当![]() ②当
②当![]() 两种情况进行讨论即可.
两种情况进行讨论即可.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,
证明![]() ,得到
,得到![]() ,求出直线
,求出直线![]() 的解析式是:
的解析式是:![]()
设![]() ,则
,则![]() ,
,![]() ,分①
,分①![]() ,②
,②![]() 两种情况进行讨论即可.
两种情况进行讨论即可.
(1). ∵抛物线![]() 过点
过点![]() ,
,![]() ,
,
∴![]()
解得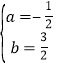
∴二次函数的表达式为:![]()
(2)抛物线![]() ,
,
当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ;
;
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
![]()
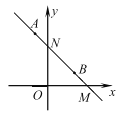
①当![]() 时,如图1,
时,如图1,![]() 点是线段
点是线段![]() 的中垂线与
的中垂线与![]() 轴的交点,
轴的交点,
设![]() ,则
,则![]() ,在
,在![]() 中,
中,
![]() ,解得
,解得![]() ,
,
∴![]()
②当![]() 时,
时, ![]()
∴![]()
(3)2或![]()
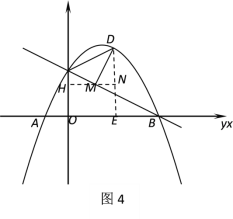
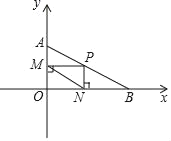
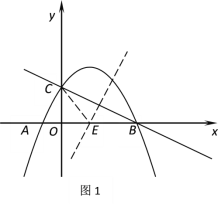
如图4,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,
易证![]()
∴![]() ,
,
在(2)的图1中![]()
∴![]()
∴![]()
![]()
∵![]() ,
,![]()
∴直线![]() 的解析式是:
的解析式是:![]()
设![]()
则![]() ,
,![]()
①当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
将![]() 代入
代入![]() 得:
得:
![]()
解得![]() ,
,![]()
∴![]() 点的横坐标是
点的横坐标是![]() .
.
②当![]() 时,
时,![]() ,
,
方法同①,可确定![]() 的横坐标时
的横坐标时![]()

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
【题目】某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是_________分,乙队成绩的众数是_________分;
(2)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是_________队;
(3)测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.