题目内容
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数，则把点M叫做“整点”．例如：P（1，0）、Q（2，﹣2）都是“整点”．抛物线y＝mx2﹣4mx+4m﹣2（m＞0）与x轴交于点A、B两点，若该抛物线在A、B之间的部分与线段AB所围成的区域（包括边界）恰有七个整点，则m的取值范围是（ ）
A. 
≤m＜1B. ＜m≤1C. 1＜m≤2D. 1＜m＜2
【答案】B
【解析】
画出图象，利用图象可得m的取值范围
∵y＝mx2﹣4mx+4m﹣2＝m（x﹣2）2﹣2且m＞0，
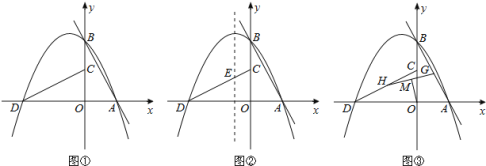
∴该抛物线开口向上，顶点坐标为（2，﹣2），对称轴是直线x＝2．
由此可知点（2，0）、点（2，﹣1）、顶点（2，﹣2）符合题意．
①当该抛物线经过点（1，﹣1）和（3，﹣1）时（如答案图1），这两个点符合题意．
将（1，﹣1）代入y＝mx2﹣4mx+4m﹣2得到﹣1＝m﹣4m+4m﹣2．解得m＝1．
此时抛物线解析式为y＝x2﹣4x+2．
由y＝0得x2﹣4x+2＝0．解得
∴x轴上的点（1，0）、（2，0）、（3，0）符合题意．
则当m＝1时，恰好有 （1，0）、（2，0）、（3，0）、（1，﹣1）、（3，﹣1）、（2，﹣1）、（2，﹣2）这7个整点符合题意．
∴m≤1．【注：m的值越大，抛物线的开口越小，m的值越小，抛物线的开口越大】
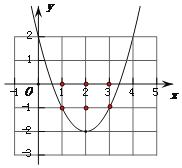
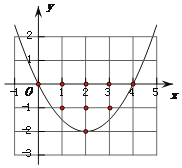
答案图1（m＝1时） 答案图2（ m＝
时）
②当该抛物线经过点（0，0）和点（4，0）时（如答案图2），这两个点符合题意．
此时x轴上的点 （1，0）、（2，0）、（3，0）也符合题意．
将（0，0）代入y＝mx2﹣4mx+4m﹣2得到0＝0﹣4m+0﹣2．解得m＝
．
此时抛物线解析式为y＝x2﹣2x．
当x＝1时，得
．∴点（1，﹣1）符合题意．
当x＝3时，得
.∴点（3，﹣1）符合题意．
综上可知：当m＝时，点（0，0）、（1，0）、（2，0）、（3，0）、（4，0）、（1，﹣1）、（3，﹣1）、（2，﹣2）、（2，﹣1）都符合题意，共有9个整点符合题意，
∴m＝不符合题．
∴m＞．
＜m≤1时，该函数的图象与x轴所围成的区域（含边界）内有七个整点，故选：B．
【题目】某校初三一班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（1）甲队成绩的中位数是_________分，乙队成绩的众数是_________分；
（2）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是_________队；
（3）测试结果中，乙队获满分的四名同学相当优秀，他们是三名男生、一名女生，现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛，用树状图或列表法求恰好抽中一男生一女生的概率.
