题目内容
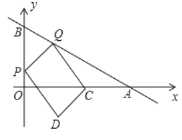
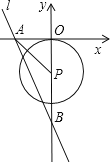
【题目】如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
(1)若⊙P与x轴有公共点,则k的取值范围是______.
(2)连接PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;
(3)当⊙P与直线l相切时,k的值为______.
【答案】(1)-3≤k<0 ;(2)⊙P与x轴相切,见解析;(3)3![]() -8或-8-3
-8或-8-3![]() .
.
【解析】
(1)P点在y轴的负半轴,且半径为3,由此可求k的取值范围;
(2)由勾股定理求PA,根据PA=PB列方程求k的值,判断⊙P与x轴的位置关系;
(3)过P点作PQ⊥AB,垂足为Q,根据△ABP的面积公式,利用面积法表示PQ,当⊙P与直线l相切时,PQ=3,列方程求k即可.
解:(1)依题意,得k的取值范围是-3≤k<0;
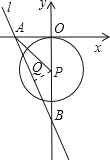
(2)由y=-2x-8得A(-4,0),B(0,-8),
由勾股定理,得PA=![]() ,
,
∵PB=8+k,
由PA=PB,得![]() =8+k,
=8+k,
解得k=-3,
∴⊙P与x轴相切;
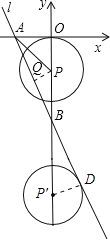
(3)过P点作PQ⊥AB,垂足为Q,
由PQ×AB=PB×OA,
PQ=![]() ,
,
当⊙P与直线l相切时,PQ=3,即![]() =3,
=3,
解得![]() ,
,
当p在B下方时,![]()
故答案为:-3≤k<0,![]() 或
或![]()

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目