��Ŀ����
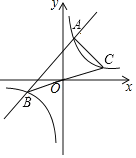
����Ŀ����ͼ��A��B��C��������λ����ͼ��ʾ��A����B�����Ϸ���180 km����C����B����ƫ��37��������֪һ�л�����A�dz�������ʻ��B�ǣ�ͬʱһ���ͳ���B�dz�������ʻ��C�ǣ�����1Сʱ��������P�أ��ͳ�����M�أ���ʱ��á�BPM��26���������ּ�����ʻ1Сʱ����������Q�أ��ͳ�����N�أ���ʱ��á�BNQ��45�������������ٶȣ����ο����ݣ�sin37����![]() ��cos37����
��cos37����![]() ��tan37����
��tan37����![]() ��sin26����
��sin26����![]() ��cos26����
��cos26����![]() ��tan26����
��tan26����![]() ��
��

���𰸡������ٶȴ�ԼΪ40 km/h���ͳ����ٶȴ�ԼΪ70 km/h
��������
��������������������.
��������ͳ����ٶȷֱ�Ϊx km/h��y km/h��
�����⣬��AP��PQ��x km��BM��MN��y km.
��ͼ������M��ME��AB������ΪE��
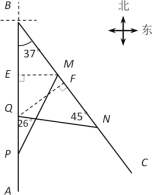
��Rt��BME��
�� sinB��![]() ���� ME��BM��sinB��y��sin37����
���� ME��BM��sinB��y��sin37����![]() y��
y��
�� cos B��![]() ���� BE��BM��cos B��y��cos37����
���� BE��BM��cos B��y��cos37����![]() y��
y��
��Rt��PME���� tan��MPE��![]() ��
��
�� PE��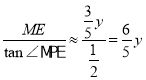
�� BE��EP��AP��AB��
�� ![]() y��
y��![]() y��x��180����x��2y��180�٣�
y��x��180����x��2y��180�٣�
����Q��QF��BN������ΪF��
��Rt��BFQ���� sinB��![]() ��
��
�� QF��BQ��sinB��(180��2x)��sin37����![]() (180��2x)��
(180��2x)��
�� cos B��![]() ,�� BF��BQ��cos B��(180��2x)��cos37����
,�� BF��BQ��cos B��(180��2x)��cos37����![]() (180��2x)��
(180��2x)��
��Rt��QFN���� tan��FNQ��![]() ���� FN��
���� FN��![]() (180��2x)��
(180��2x)��
�� BF��FN��BN��
�� ![]() (180��2x)��
(180��2x)��![]() (180��2x)��2y����7x��5y��630�ڣ�
(180��2x)��2y����7x��5y��630�ڣ�
�ɢ٢ڣ���x��40
�𣺻����ٶȴ�ԼΪ40 km/h���ͳ����ٶȴ�ԼΪ70 km/h��