题目内容
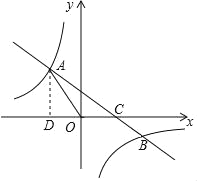
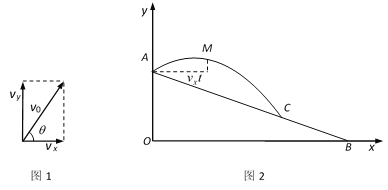
【题目】如图1，已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy，θ是水龙头的仰角，且
．图2是一个建在斜坡上的花圃场地的截面示意图，水龙头的喷射点A在山坡的坡顶上（喷射点离地面高度忽略不计），坡顶的铅直高度OA为15米，山坡的坡比为
．离开水龙头后的水（看成点）获得初始速度v0米/秒后的运动路径可以看作是抛物线，点M是运动过程中的某一位置．忽略空气阻力，实验表明：M与A的高度之差d（米）与喷出时间t（秒）的关系为
；M与A的水平距离为
米．已知该水流的初始速度
为15米/秒，水龙头的仰角θ为
．
（1）求水流的横向初始速度vx和纵向初始速度vy；
（2）用含t的代数式表示点M的横坐标x和纵坐标y，并求y与x的关系式（不写x的取值范围）；
（3）水流在山坡上的落点C离喷射点A的水平距离是多少米？若要使水流恰好喷射到坡脚B处的小树，在相同仰角下，则需要把喷射点A沿坡面AB方向移动多少米？
【答案】（1）水流的横向初始速度vx是9米/秒，纵向初始速度vy是12米/秒;
（2）y＝
x2＋
x＋15；（3）
.
【解析】
（1）根据题意利用θ的正弦和余弦定义可得结论；
（2）由（1）的vx表示出x，OA已知，利用y＝d＋OA，代入OA的值和d与t的函数关系式，可以得解；
（3）先求得点A和点B的坐标，进而写出其直线解析式，再将其与（2）中抛物线解析式联立，从而求得落点C的坐标，再利用平移知识及勾股定理可以求解．
解：（1）∵v0为15米/秒，水龙头的仰角θ为53°，
∴cosθ＝
，sinθ＝
，
∴vx＝15cos53°＝15
＝9，vy＝15sin53°＝15×
＝12；
答：水流的横向初始速度vx是9米/秒，纵向初始速度vy是12米/秒；
（2）x＝vxt＝9t，
∴t＝
，
又M与A的高度之差d（米）与喷出时间t（秒）的关系为d＝vyt5t2，
∴y＝d＋OA＝12t5t2＋15＝5×()2＋12×＋15＝x2＋x＋15；
∴y与x的关系式为：y＝x2＋x＋15；
（3）∵坡顶的铅直高度OA为15米，山坡的坡比为
，
∴OB＝45米，点A（0，15）点B（45，0）
∴直线AB的解析式为：y＝x＋15，
将其与抛物线解析式联立得：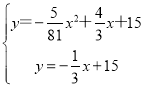
，
解得：
（舍）或
，
∴水流在山坡上的落点C坐标为（27，6），喷射点A沿坡面AB方向移动的距离等于BC的距离，而BC＝
米，
答：水流在山坡上的落点C离喷射点A的水平距离是27米，需要把喷射点A沿坡面AB方向移动米．
