题目内容
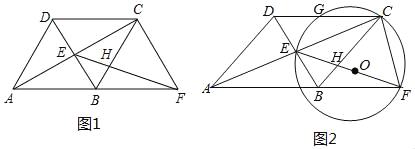
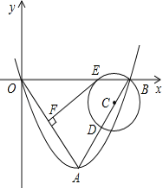
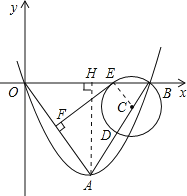
【题目】如图,平面直角坐标系中点A坐标为(2,﹣4),以A为顶点的抛物线经过坐标原点交x轴于点B.
(1)求抛物线的解析式;
(2)取线段AB上一点D,以BD为直径作⊙C交x轴于点E,作EF⊥AO于点F,
求证:EF是⊙C的切线;
(3)设⊙C的半径为r,EF=m,求m与r的函数关系式及自变量r的取值范围.
【答案】(1)y=x2﹣4x;(2)证明见解析;(3) ![]() .
.
【解析】
(1)结合已知条件可以知道抛物线经过A(2,-4),O(0,0),代入解析式,即可求出抛物线的解析式;
(2)连接CE,只要求证CE∥AO,结合已知推出EF⊥CE,即可求证出结论;
(3)作AH⊥OB于H点,结合勾股定理和抛物线的性质求出个线段的长度,根据平行线的性质,写出比例式,求出半径CB的长度
(1)设y=a(x﹣2)2﹣4,把O(0,0)代入,得4a﹣4=0,
∴a=1,
∴y=(x﹣2)2﹣4=y=x2﹣4x;
(2)连接CE,
∴CE=CB
∴∠CEB=∠CBE
∵抛物线有对称性
∴AO=AB
∴∠AOB=∠OBA
∴∠AOB=∠CEB
∴CE∥AO
∵EF⊥AO
∴EF⊥CE
∴EF是⊙C的切线
(3)作AH⊥OB于H,∴OH=HB=2,AH=4,AO=AB=![]()
∴sin∠AOB=sin∠ABO=![]()
在RT△EFO中,EF=OEsin∠BOA=![]()
由(2)CE∥OA,∴△BEC∽△BOA,
∴![]() ,即
,即![]()
∴BE=![]()
∴OE=OB﹣EB=![]()
∴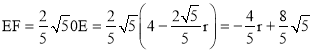
即:![]() ,
,
∴0<r<![]() .
.

练习册系列答案
相关题目