题目内容
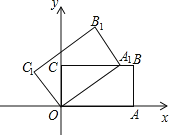
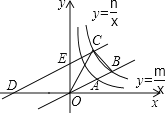
【题目】如图,直线y=![]() x分别与双曲线y=
x分别与双曲线y=![]() 和y=
和y=![]() 交于第一象限内的点A和B,且OA=2AB,将直线y=
交于第一象限内的点A和B,且OA=2AB,将直线y=![]() x向左平移4个单位后,分别与x轴,y轴交于点D、E,与双曲线y=
x向左平移4个单位后,分别与x轴,y轴交于点D、E,与双曲线y=![]() 交于点C,△OBC的面积为3.
交于点C,△OBC的面积为3.
(1)求m,n的值;
(2)点C到直线AB的距离是 .
【答案】(1)m=2,n=![]() ;(2)
;(2)![]()
【解析】
(1)根据直线解析式平移的规律得出y=![]() x向左平移4个单位后的解析式为y=
x向左平移4个单位后的解析式为y=![]() x+2,那么交y轴于E(0,2).作EF⊥OB于F,根据互相垂直的两直线斜率之积为-1且过点E,得到直线EF的解析式为y=-2x+2,与y=
x+2,那么交y轴于E(0,2).作EF⊥OB于F,根据互相垂直的两直线斜率之积为-1且过点E,得到直线EF的解析式为y=-2x+2,与y=![]() x联立,求出F(
x联立,求出F(![]() ,
,![]() ),根据两点间的距离公式得出EF=
),根据两点间的距离公式得出EF=![]() ,根据S△OBC=3,求出OB=
,根据S△OBC=3,求出OB=![]() ,由OA=2AB=
,由OA=2AB=![]() OB=
OB=![]() ,得出A(2,1),B(3,
,得出A(2,1),B(3,![]() ),将点A和B的坐标分别代入y=
),将点A和B的坐标分别代入y=![]() 和y=
和y=![]() ,即可求出m,n的值;
,即可求出m,n的值;
(2)点C到直线AB的距离等于EF的长.
(1)直线y=![]() x向左平移4个单位后的解析式为y=
x向左平移4个单位后的解析式为y=![]() (x+4),即y=
(x+4),即y=![]() x+2,
x+2,
∴直线y=![]() x+2交y轴于E(0,2),
x+2交y轴于E(0,2),
如图,作EF⊥OB于F,
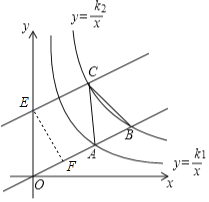
可得直线EF的解析式为y=﹣2x+2,
由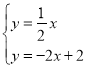 ,解得
,解得![]() ,
,
∴F(![]() ,
,![]() ),
),
∴EF=![]() =
=![]() ,
,
∵S△OBC=3,
∴![]() OBEF=3,
OBEF=3,
∴OB=![]() ,
,
∵OA=2AB=![]() OB=
OB=![]() ,
,
∴A(2,1),B(3,![]() ),
),
∴m=2,n=![]() ;
;
(2)∵CE∥OB,EF⊥OB于F,
∴点C到直线AB的距离=EF=![]() .
.
故答案为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了实现伟大的强国复兴梦,全社会都在开展“扫黑除恶”专项斗争,某区为了解各学校老师对“扫黑除恶”应知应会知识的掌握情况,对甲、乙两个学校各180名老师进行了测试,从中各随机抽取30名教师的成绩(百分制),并对成绩(单位:分)进行整理、描述和分析,给出了部分成绩信息.
成绩(分) 频数 学校 | 90≤x<92 | 92≤x<94 | 94≤x<96 | 96≤x<98 | 98≤x≤100 |
甲校 | 2 | 3 | 5 | 10 | 10 |
甲校参与测试的老师成绩在96≤x<98这一组的数据是:96,96.5,97,97.5,97,96.5,97.5,96,96.5,96.5
甲、乙两校参与测试的老师成绩的平均数平均数、中位数、众数如下表:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 96.35 | m分 | 99分 |
乙校 | 95.85 | 97.5份 | 99分 |
根据以上信息,回答下列问题:
(1)m= ;
(2)在此次随机抽样测试中,甲校的王老师和乙校的李老师成绩均为97分,则在各自学校参与测试老师中成绩的名次相比较更靠前的是 (填“王”或“李”)老师,请写出理由;
(3)在此次随机测试中,乙校96分以上(含96分)的总人数比甲校96分以上(含96分)的总人数的2倍少100人,试估计乙校96分以上(含96分)的总人数.