题目内容
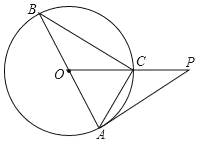
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线AP与OC的延长线相交于点P,∠P=∠BCO.
(1)求证:AC=PC;
(2)若AB=6![]() ,求AP的长.
,求AP的长.
【答案】(1)详见解析;(2)9.
【解析】
(1)根据切线的性质得到∠B=∠CAP,根据等腰三角形的判定定理证明;
(2)证明△AOC为等边三角形,根据正切的定义计算,得到答案.
(1)证明:∵AP是⊙O的切线,
∴∠B=∠CAP,
∵OB=OC,
∴∠B=∠OCB,
∴∠OCB=∠CAP,
∵∠P=∠BCO,
∴∠P=∠CAP,
∴AC=PC;
(2)解:∠AOC=2∠BCO,∠ACO=2∠P,
∴∠AOC=∠ACO,
∴AC=AO,
∵OA=OC,
∴△AOC为等边三角形,
∴AP=OAtan∠AOC=9.

练习册系列答案
相关题目