题目内容
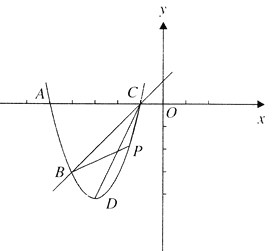
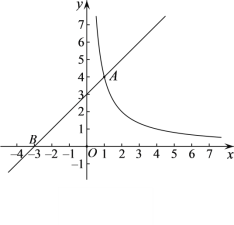
【题目】如图,直线![]() 与函数
与函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
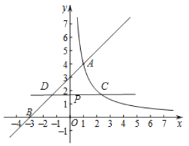
(2)过动点![]() 作平行于
作平行于![]() 轴的直线,交函数
轴的直线,交函数![]() 的图象于点
的图象于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() . (2)①
. (2)①![]() . ②
. ②![]() 或
或![]() .
.
【解析】
(1)把A(1,m)代入直线![]() ,可求得m的值;把A(1,m)代入直线
,可求得m的值;把A(1,m)代入直线![]() ,即可求得k的值;
,即可求得k的值;
(2))①利用C、D的纵坐标都为2得到C点和D点的横坐标,然后求两横坐标之差得到线段CD的长;
②先确定B(-3,0),由于C、D的纵坐标都为n,根据一次函数和反比例函数图象上点的坐标特征可表示出C(![]() ,n),D(n-3,3),讨论:当点C在点D的右侧时,先利用CD=OB得到
,n),D(n-3,3),讨论:当点C在点D的右侧时,先利用CD=OB得到![]() ,解得
,解得![]() 2,
2,![]() -2(舍去),再结合图象可判断当0<n≤2时,CD≥OB;当点C在点D的左侧时,先利用CD=OB得到
-2(舍去),再结合图象可判断当0<n≤2时,CD≥OB;当点C在点D的左侧时,先利用CD=OB得到![]() ,解得
,解得![]() 3+
3+![]() ,
,![]() 3-
3-![]() (舍去),再结合图象即可求解.
(舍去),再结合图象即可求解.
(1)∵直线![]() 经过点A(1,m),
经过点A(1,m),
∴![]() ,
,
又∵函数![]() 的图象经过点A(1,4),
的图象经过点A(1,4),
∴![]() ;
;
(2)①当![]() 时,点
时,点![]() 的坐标为(0,2),
的坐标为(0,2),
∴点C的坐标为(2,2),
点D的坐标为(-1,2),
∴![]() ;
;
②当![]() 时,
时,![]() ,解得
,解得![]() ,则B(-3,0),
,则B(-3,0),
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
∴点C的坐标为(![]() ,
,![]() ),
),
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴点D的坐标为(![]() ,
,![]() ),
),
当点C在点D的右侧时,
若CD=OB,即![]() ,解得
,解得![]() ,
,![]() (舍去),
(舍去),
∴当![]() 时,CD≥OB;
时,CD≥OB;
当点C在点D的左侧时,
若CD=OB,即![]() ,解得
,解得![]() ,
,![]() (舍去),
(舍去),
∴当![]() 时,CD
时,CD![]() OB,
OB,
综上所述,![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
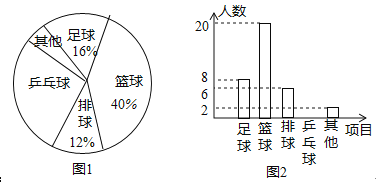
小学生10分钟应用题系列答案【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
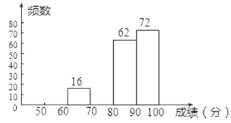
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
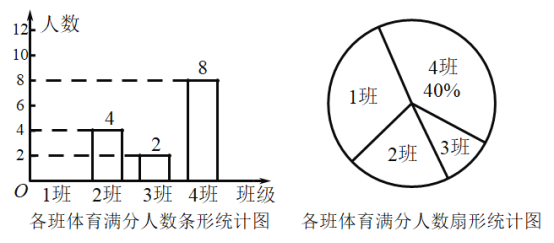
【题目】我市各学校积极响应上级“停课不停教、修课不停学”的要求,开展了空中在线教学.其校就“网络直播课”的满意度进行了随机在线问卷调在,调在结果分为四类: A.非常满意;B.很满意;C.一般;D.不满意,将收集到的信息进行了统计,绘制成如下不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题:
(1)接受问卷调查的学生共有__ _人;![]() ;
;![]() ;
;
(2)补全条形统计图;
频数分布统计表
类别 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
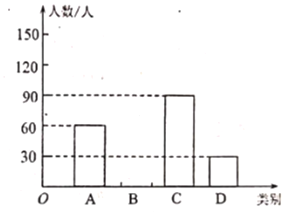
(3)若该校共有学生![]() 人,请你根据上述调查结果,估计该校对“网络直播课”满意度为
人,请你根据上述调查结果,估计该校对“网络直播课”满意度为![]() 类和
类和![]() 类的学生共有多少人;
类的学生共有多少人;
(4)为改进教学,学校决定从选填结果是![]() 类的学生中,选取甲、乙、丙、丁四人,随机抽取两名同学参与网络座谈会,求甲、乙两名同学同时被抽中的概率.
类的学生中,选取甲、乙、丙、丁四人,随机抽取两名同学参与网络座谈会,求甲、乙两名同学同时被抽中的概率.
【题目】我市各学校积极响应上级“停课不停教、修课不停学”的要求,开展了空中在线教学.其校就“网络直播课”的满意度进行了随机在线问卷调在,调在结果分为四类: A.非常满意;B.很满意;C.一般;D.不满意,将收集到的信息进行了统计,绘制成如下不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题:
(1)接受问卷调查的学生共有__ _人;![]() ;
;![]() ;
;
(2)补全条形统计图;
频数分布统计表
类别 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
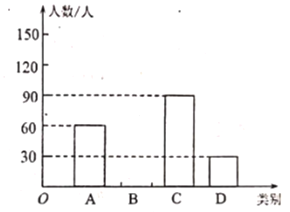
(3)若该校共有学生![]() 人,请你根据上述调查结果,估计该校对“网络直播课”满意度为
人,请你根据上述调查结果,估计该校对“网络直播课”满意度为![]() 类和
类和![]() 类的学生共有多少人;
类的学生共有多少人;
(4)为改进教学,学校决定从选填结果是![]() 类的学生中,选取甲、乙、丙、丁四人,随机抽取两名同学参与网络座谈会,求甲、乙两名同学同时被抽中的概率.
类的学生中,选取甲、乙、丙、丁四人,随机抽取两名同学参与网络座谈会,求甲、乙两名同学同时被抽中的概率.