题目内容
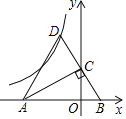
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠BAC=30°,点A的坐标为(﹣3,0),将△ABC沿直线AC翻折,点B的对应点D恰好落在反比例函数![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
A. 2![]() B. ﹣2
B. ﹣2![]() C. 4
C. 4![]() D. ﹣4
D. ﹣4![]()
【答案】B
【解析】
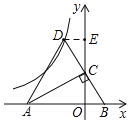
如图,过点D作DE⊥y轴于点E.由对称可知CD=BC,易证△DCE≌△BCO(AAS),所以CE=CO,DE=OB,由∠BAC=30°,OA=3,所以OC=![]() OA=
OA=![]() ,∠OCB=30°,所以OB=
,∠OCB=30°,所以OB=![]() OC=1,于是DE=OB=1,CE=OC=
OC=1,于是DE=OB=1,CE=OC=![]() ,OE=2
,OE=2![]() ,|k|=DEOE=1×2
,|k|=DEOE=1×2![]() =2
=2![]() ,反比例函数图象在第二象限,因此k=﹣2
,反比例函数图象在第二象限,因此k=﹣2![]() .
.
解:如图,过点D作DE⊥y轴于点E.
由对称可知CD=BC,
易证△DCE≌△BCO(AAS),
∴CE=CO,DE=OB,
∵∠BAC=30°,OA=3
∴OC=![]() OA=
OA=![]() ,
,
∠OCB=30°,
∴OB=![]() OC=1,
OC=1,
∴DE=OB=1,CE=OC=![]() ,OE=2
,OE=2![]() ,
,
|k|=DEOE=1×2![]() =2
=2![]() ,
,
∵反比例函数图象在第二象限,
∴k=﹣2![]() ,
,
故选:B.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目