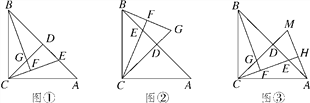
ƒøƒ⁄»ð
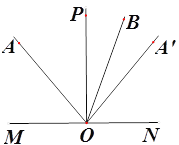
°æƒø°ø»ÁÕº£¨∆Ω√ʃ⁄“ª∂®µ„A‘⁄÷±œþMNµƒ…œ∑Ω£¨µ„OŒ™÷±œþMN…œ“ª∂ص„ £¨◊˜…‰œþOA°¢OP°¢OA°Ø£¨µ±µ„O‘⁄÷±œþMN…œ‘À∂Ø ±£¨ º÷’±£≥÷°œMOP=90°„°¢°œAOP=°œA°ØOP£¨Ω´…‰œþOA»∆µ„OÀ≥ ±’Ζ˝◊™60°„µ√µΩ…‰œþOB
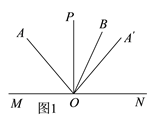
£®1£©»ÁÕº£¨µ±µ„O‘À∂ØµΩ πµ„A‘⁄…‰œþOPµƒ◊Û≤ý£¨»ÙOB∆Ω∑÷°œA°ØOP£¨«Û°œAOPµƒ∂» ˝£ª
£®2£©µ±µ„O‘À∂ØµΩ πµ„A‘⁄…‰œþOPµƒ◊Û≤ý£¨°œAOM=3°œA°ØOB ±£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©µ±µ„O‘À∂ØµΩƒ≥“ª ±øà ±£¨°œA°ØOB=150°„£¨÷±Ω”–¥≥ˆ°œBOP= ∂».
°æ¥∞∏°ø(1) °œAOP=40°„£ª(2) ![]() ªÚ6£ª (3) 105ªÚ135.
ªÚ6£ª (3) 105ªÚ135.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫
£®1£©”…“‚“◊µ√£∫°œAOB=60°„£¨°œAOP=°œA°‰OP=2°œPOB£¨”…¥Àø…µ√°œAOP+°œPOB=3°œPOB=60°„£¨’‚—˘Ω‚µ√°œPOB=20°„£¨º¥ø…µ√µΩ°œAOP=40°„£ª
£®2£©¢Ÿµ±…‰œþOB‘⁄°œA°‰OPµƒƒ⁄≤ø ±£¨»ÁÕº1£¨…Ë°œA°‰OB= ![]() £¨‘Ú°œAOM=
£¨‘Ú°œAOM=![]() £¨°œAON=
£¨°œAON=![]() £¨°œAOA°‰=
£¨°œAOA°‰= ![]() £¨”…¥Àø…µ√°œAOP=°œA°‰OP=
£¨”…¥Àø…µ√°œAOP=°œA°‰OP=![]() £¨”…°œAOM+°œAOP=°œMOP=90°„ø…µ√
£¨”…°œAOM+°œAOP=°œMOP=90°„ø…µ√![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨”…¥Àº¥ø…«Ûµ√°œAON∫Õ°œAOP£¨¥”∂¯ø…«Ûµ√À¸√«µƒ±»÷µ£ª
£¨”…¥Àº¥ø…«Ûµ√°œAON∫Õ°œAOP£¨¥”∂¯ø…«Ûµ√À¸√«µƒ±»÷µ£ª
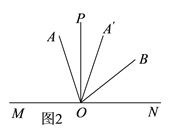
¢⁄µ±…‰œþOB‘⁄°œAONµƒƒ⁄≤ø ±£¨»ÁÕº2£¨…Ë°œA°‰OB= ![]() £¨‘Ú°œAOM=
£¨‘Ú°œAOM=![]() £¨°œAON=
£¨°œAON=![]() £¨°œAOA°‰=
£¨°œAOA°‰= ![]() £¨”…¥Àø…µ√°œAOP=°œA°‰OP=
£¨”…¥Àø…µ√°œAOP=°œA°‰OP=![]() £¨”…°œAOM+°œAOP=°œMOP=90°„ø…µ√
£¨”…°œAOM+°œAOP=°œMOP=90°„ø…µ√![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨”…¥Àº¥ø…«Ûµ√°œAON∫Õ°œAOP£¨¥”∂¯ø…«Ûµ√À¸√«µƒ±»÷µ£ª
£¨”…¥Àº¥ø…«Ûµ√°œAON∫Õ°œAOP£¨¥”∂¯ø…«Ûµ√À¸√«µƒ±»÷µ£ª
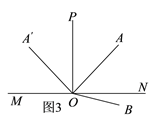
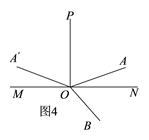
£®3£©»ÁÕº3£¨µ±°œA°‰OB=150°„ ±£¨“◊µ√°œA°‰OA=150°„-60°„=90°„£¨Ω·∫œ°œAOP=°œA°‰OPø…µ√°œAOP=45°„£¨¥”∂¯ø…µ√°œBOP=60°„+45°„=105°„£ª»ÁÕº4£¨µ±°œA°‰OB=150°„ ±£¨“◊µ√°œA°‰OA=360°„-150°„-60°„=150°„£¨Ω·∫œ°œAOP=°œA°‰OPø…µ√°œAOP=75°„£¨¥”∂¯ø…µ√°œBOP=60°„+75°„=135°„£ª
‘Ã‚Ω‚Œˆ£∫
£®1£©”…“‚ø…µ√£∫°œAOB=60°„£¨°œAOP=°œA°‰OP£¨
°þOB∆Ω∑÷°œA°‰OP£¨
°ý°œA°‰OP=2°œPOB£¨
°ý°œAOP=°œA°‰OP=2°œPOB£¨
°ý°œAOB=°œAOP+°œPOB=3°œPOB=60°„£¨
°ý°œPOB=20°„£¨
°ý°œAOP=2°œPOB=40°„£ª
(2)¢Ÿµ±µ„O‘À∂ØµΩ πµ„A‘⁄…‰œþOPµƒ◊Û≤ý£¨«“…‰œþOB‘⁄‘⁄°œA°‰OPµƒƒ⁄≤ø ±£¨»ÁÕº1£¨
…Ë°œA°‰OB=x£¨‘Ú°œAOM=3°œA°‰OB=3x£¨°œAOA°‰= ![]() £¨
£¨
°þOP°ÕMN£¨
°ý°œAON=180°„-3£¨°œAOP=90°„-3x£¨
°ý![]() £¨
£¨
°þ°œAOP=°œA°‰OP£¨
°ý°œAOP=°œA°‰OP=![]()
°ý![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫ ![]() £¨
£¨
°ý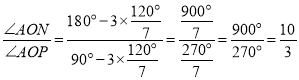 £ª
£ª
¢⁄µ±µ„O‘À∂ØµΩ πA‘⁄…‰œþOPµƒ◊Û≤ý£¨µ´ «…‰œþOB‘⁄°œA°‰ONƒ⁄≤ø ±£¨»ÁÕº2£¨
…Ë°œA°‰OB=x£¨‘Ú°œAOM=3x£¨°œAON=![]() £¨°œAOA°‰=
£¨°œAOA°‰= ![]() £¨
£¨
°þ°œAOP=°œA°‰OP£¨
°ý°œAOP=°œA°‰OP=![]() £¨
£¨
°þOP°ÕMN£¨
°ý°œAOP=90-°œAOM=90-3x£¨
°ý![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫ ![]() £¨
£¨
°ý![]() £ª
£ª
£®3£©¢Ÿ»ÁÕº3£¨µ±°œA°‰OB=150°„ ±£¨
”…Õºø…µ√£∫°œA°‰OA=°œA°‰OB-°œAOB=150°„-60°„=90°„£¨
”÷°þ°œAOP=°œA°‰OP£¨
°ý°œAOP=45°„£¨
°ý°œBOP=60°„+45°„=105°„£ª
¢⁄»ÁÕº4£¨µ±°œA°‰OB=150°„ ±£¨”…Õºø…µ√°œA°‰OA=360°„-150°„-60°„=150°„£¨
”÷°þ°œAOP=°œA°‰OP£¨
°ý°œAOP=75°„£¨
°ý°œBOP=60°„+75°„=135°„£ª
◊€…œÀ˘ ˆ£∫°œBOPµƒ∂» ˝Œ™105°„ªÚ135°„.

°æƒø°ø ¢ ¢Õ¨—ßµΩƒ≥∏þ–£”ŒÕÊ ±£¨ø¥µΩ‘À∂Ø≥°µƒ–˚¥´¿∏÷–µƒ≤ø∑÷–≈œ¢£®»Áœ¬±Ì£©£∫
‘∫œµ¿∫«Ú»¸≥…º®π´∏Ê | |||
±»»¸≥°¥Œ | §≥° | ∏∫≥° | ª˝∑÷ |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
¢ ¢Õ¨—ßΩ·∫œ—ßœ∞µƒ÷™ ∂…˺∆¡À»Áœ¬Œ £¨«Îƒ„∞Ô√¶ÕÍ≥…œ¬¡–Œ £∫
£®1£©¥”±Ì÷–ø…“‘ø¥≥ˆ£¨∏∫“ª≥°ª˝______∑÷, §“ª≥°ª˝_______∑÷£ª
£®2£©ƒ≥∂”‘⁄±»ÕÍ22≥°µƒ«∞÷œ¬£¨ §≥°◊Ъ˝∑÷ƒÐµ»”⁄∆‰∏∫≥°◊Ъ˝∑÷µƒ2±∂¬£ø«ÎÀµ√˜¿Ì”….