ÌâÄ¿ÄÚÈÝ
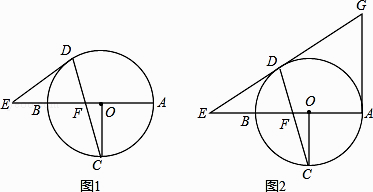
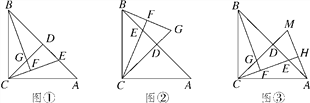
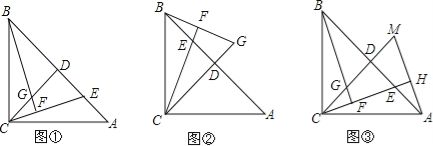
¡ŸÌâÄ¿¡¿ÈçÍŒ¢Ù£¬ÔÚ¡÷ABCÖУ¬AC£œBC£¬¡ÏACB£œ90¡ã£¬¹ýµãC×÷CD¡ÍABÓÚµãD£¬µãEÊÇAB±ßÉÏÒ»¶¯µã(²»º¬¶ËµãA£¬B)£¬Á¬œÓCE£¬¹ýµãB×÷CEµÄŽ¹Ïßœ»Ö±ÏßCEÓÚµãF£¬œ»Ö±ÏßCDÓÚµãG.
(1)ÇóÖ€£ºAE£œCG£»
(2)ÈôµãEÔ˶¯µœÏ߶ÎBDÉÏʱ(ÈçÍŒ¢Ú)£¬ÊÔ²ÂÏëAE£¬CGµÄÊýÁ¿¹ØϵÊÇ·ñ·¢Éú±ä»¯£¬ÇëÐŽ³öÄãµÄœáÂÛ£»
(3)¹ýµãA×÷AH¡ÍCE£¬Ž¹×ãΪµãH£¬²¢œ»CDµÄÑÓ³€ÏßÓÚµãM(ÈçÍŒ¢Û)£¬ÕÒ³öÍŒÖÐÓëBEÏàµÈµÄÏ߶Σ¬²¢Ö€Ã÷£®
¡ŸŽð°ž¡¿£š1£©ŒûœâÎö£»£š2£©²»±ä£»£š3£©BE£œCM.
¡ŸœâÎö¡¿ÊÔÌ⣚1£©ÈçÍŒ¢Ù£¬žùŸÝµÈÑüÖ±œÇÈýœÇÐεÄÐÔÖÊ¿ÉÒԵóö¡ÏBCD=¡ÏACD=45¡ã£¬žùŸÝÖ±œÇÈýœÇÐεÄÈýœÇÐεÄÐÔÖÊŸÍ¿ÉÒԵóö¡ÏCBF=¡ÏACE£¬ÓÉASAŸÍ¿ÉÒԵóö¡÷BCG¡Õ¡÷CAE£¬ŸÍ¿ÉÒԵóöœáÂÛ£»
£š2£©ÈçÍŒ¢Ú£¬žùŸÝµÈÑüÖ±œÇÈýœÇÐεÄÐÔÖÊ¿ÉÒԵóö¡ÏBCD=¡ÏACD=45¡ã£¬žùŸÝÖ±œÇÈýœÇÐεÄÈýœÇÐεÄÐÔÖÊŸÍ¿ÉÒԵóö¡ÏCBF=¡ÏACE£¬ÓÉASAŸÍ¿ÉÒԵóö¡÷BCG¡Õ¡÷CAE£¬ŸÍ¿ÉÒԵóöœáÂÛ£»
£š3£©ÈçÍŒ¢Û£¬žùŸÝµÈÑüÖ±œÇÈýœÇÐεÄÐÔÖÊ¿ÉÒԵóö¡ÏBCD=¡ÏACD=45¡ã£¬žùŸÝÖ±œÇÈýœÇÐεÄÈýœÇÐεÄÐÔÖÊŸÍ¿ÉÒԵóö¡ÏBCE=¡ÏCAM£¬ÓÉASAŸÍ¿ÉÒԵóö¡÷BCE¡Õ¡÷CAM£¬ŸÍ¿ÉÒԵóöœáÂÛ£»
œâ£º£š1£©¡ßAC=BC£¬
¡à¡ÏABC=¡ÏCAB£®
¡ß¡ÏACB=90¡ã£¬
¡à¡ÏABC=¡ÏA=45¡ã£¬¡ÏACE+¡ÏBCE=90¡ã£®
¡ßBF¡ÍCE£¬
¡à¡ÏBFC=90¡ã£¬
¡à¡ÏCBF+¡ÏBCE=90¡ã£¬
¡à¡ÏACE=¡ÏCBF
¡ßÔÚRT¡÷ABCÖУ¬CD¡ÍAB£¬AC=BC£¬
¡à¡ÏBCD=¡ÏACD=45¡ã
¡à¡ÏA=¡ÏBCD£®
ÔÚ¡÷BCGºÍ¡÷ACEÖÐ
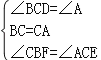 £¬
£¬
¡à¡÷BCG¡Õ¡÷ACE£šASA£©£¬
¡àAE=CG£»
£š2£©²»±ä£®AE=CG£®
ÀíÓÉ£º¡ßAC=BC£¬
¡à¡ÏABC=¡ÏCAB£®
¡ß¡ÏACB=90¡ã£¬
¡à¡ÏABC=¡ÏA=45¡ã£¬¡ÏACE+¡ÏBCE=90¡ã£®
¡ßBF¡ÍCE£¬
¡à¡ÏBFC=90¡ã£¬
¡à¡ÏCBF+¡ÏBCE=90¡ã£¬
¡à¡ÏACE=¡ÏCBF
¡ßÔÚRT¡÷ABCÖУ¬CD¡ÍAB£¬AC=BC£¬
¡à¡ÏBCD=¡ÏACD=45¡ã
¡à¡ÏA=¡ÏBCD£®
ÔÚ¡÷BCGºÍ¡÷ACEÖÐ
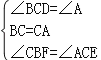 £¬
£¬
¡à¡÷BCG¡Õ¡÷ACE£šASA£©£¬
¡àAE=CG£»
£š3£©BE=CM£¬
£º¡ßAC=BC£¬
¡à¡ÏABC=¡ÏCAB£®
¡ß¡ÏACB=90¡ã£¬
¡à¡ÏABC=¡ÏA=45¡ã£¬¡ÏACE+¡ÏBCE=90¡ã£®
¡ßAH¡ÍCE£¬
¡à¡ÏAHC=90¡ã£¬
¡à¡ÏHAC+¡ÏACE=90¡ã£¬
¡à¡ÏBCE=¡ÏHAC£®
¡ßÔÚRT¡÷ABCÖУ¬CD¡ÍAB£¬AC=BC£¬
¡à¡ÏBCD=¡ÏACD=45¡ã
¡à¡ÏACD=¡ÏABC£®
ÔÚ¡÷BCEºÍ¡÷CAMÖÐ
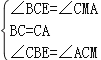 £¬
£¬
¡à¡÷BCE¡Õ¡÷CAM£šASA£©£¬
¡àBE=CM£®

 ÌìÌìÏòÉÏÒ»±ŸºÃŸíϵÁÐŽð°ž
ÌìÌìÏòÉÏÒ»±ŸºÃŸíϵÁÐŽð°ž СѧÉú10·ÖÖÓÓŠÓÃÌâϵÁÐŽð°ž
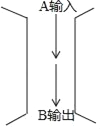
СѧÉú10·ÖÖÓÓŠÓÃÌâϵÁÐŽð°ž¡ŸÌâÄ¿¡¿ÈçÍŒ£¬Ä³ŒÆËã×°ÖÃÓÐÒ»µŸÝÊäÈë¿ÚAºÍÒ»ÔËËãœá¹ûµÄÊä³ö¿ÚB£¬±ížñÖÐÊÇСÃ÷ÊäÈëµÄһЩÊýŸÝºÍÕâЩÊýŸÝŸžÃ×°ÖÃŒÆËãºóÊä³öµÄÏàÓŠœá¹û£¬°ŽÕÕÕâžöŒÆËã×°ÖõČÆËã¹æÂÉ£¬ÈôÊäÈëµÄÊýÊÇ10£¬ÔòÊä³öµÄÊýÊÇ£š¡¡¡¡£©
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102
¡ŸÌâÄ¿¡¿ÀîͬѧÿÌìÉÏѧ¡¢·ÅѧʹÓù«œ»¿š³Ë×ø¹«œ»³µ£¬¹«œ»¿šµÄÓà¶îÊÇ100Ôª£®Èç¹û³Ë³µŽÎÊýÓÃ![]() ±íÊŸ£¬¹«œ»¿šÉϵÄÓà¶îÓÃ
±íÊŸ£¬¹«œ»¿šÉϵÄÓà¶îÓÃ![]() ±íÊŸ£®
±íÊŸ£®
ŽÎÊý | Óà¶î |
1 |
|
2 |
|
3 |
|
¡ | ¡ |
(1)ÇëÄãžùŸÝ±ížñÖеÄÐÅÏ¢£¬ŒÆËã³öµÚ4ŽÎ³Ë³µºó£¬¹«œ»¿šÉϵÄÓà¶î£»
(2)ÇëÄãÐŽ³öÀîͬѧ¹«œ»¿šÉϵÄÓà¶î![]() Óë³Ë³µŽÎÊý
Óë³Ë³µŽÎÊý![]() µÄ¹Øϵʜ£»
µÄ¹Øϵʜ£»
(3)Çë°ïÀîͬѧŒÆËã³Ë20ŽÎ³µºó£¬¹«œ»¿šÉÏÓà¶îÊǶàÉÙÔª£®