题目内容
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F. 
(1)求证:直线EF是⊙O的切线;
(2)CF=5,cos∠A= ![]() ,求AE的长.
,求AE的长.
【答案】
(1)证明:如图,连结OD.
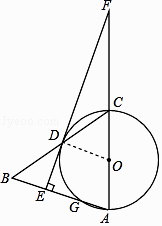
∵CD=DB,CO=OA,
∴OD是△ABC的中位线,
∴OD∥AB,AB=2OD,
∵DE⊥AB,
∴DE⊥OD,即OD⊥EF,
∴直线EF是⊙O的切线
(2)解:∵OD∥AB,
∴∠COD=∠A.
在Rt△DOF中,∵∠ODF=90°,
∴cos∠A=cos∠FOD= ![]() =
= ![]() ,
,
设⊙O的半径为R,则 ![]() =
= ![]() ,
,
解得R= ![]() ,
,
∴AB=2OD= ![]() .
.
在Rt△AEF中,∵∠AEF=90°,
∴cos∠A= ![]() =
= ![]() =
= ![]() ,
,
∴AE= ![]()
【解析】(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;(2)根据平行线的性质得到∠COD=∠A.由cos∠A=cos∠FOD= ![]() =
= ![]() ,设⊙O的半径为R,于是得到
,设⊙O的半径为R,于是得到 ![]() =
= ![]() ,解得R=
,解得R= ![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.

【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102