��Ŀ����
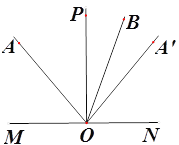
����Ŀ����ͼ����������A��B���㣬�ֱ��Ӧ����Ϊa��b����֪��a+1��2��|b��3|��Ϊ�෴������PΪ������һ���㣬��ӦΪx��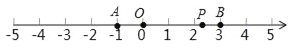
��1��a=������b=�� ��
��2������P����A�͵�B�ľ�����ȣ����P��Ӧ�������� ��
��3���������Ƿ���ڵ�P��ʹ��P����A�͵�B�ľ���֮��Ϊ5�������ڣ������x��ֵ���������ڣ�˵�����ɣ�
��4��|x��a|+|x��b|����Сֵ=�� ��
��5������P��ÿ����1����λ���ȵ��ٶȴ�O�������˶�����A��ÿ����5����λ���������˶����ʼ�����ʱ��P����A����B�ľ�����ȣ�
���𰸡�(1) ��1��3��(2)1;(3) x1=��1.5��x2=3.5��(4)4;(5) ![]() ����ʱ��P����A����B�ľ������
����ʱ��P����A����B�ľ������
��������
��1�����ݣ�a+1��2��|b-3|��Ϊ�෴�����������a��b��ֵ��
��2������������Եõ�����x�ķ��̣��Ӷ��������x��ֵ��
��3��������������г�����x�ķ��̣�������Խ����
��4���������⣬���÷������۵�˼����Խ���⣻
��5��������������г���Ӧ�ķ��̣�������Խ��.
��:��1���ߣ�a+1��2��|b��3|��Ϊ�෴����
��a+1=0��b��3=0��
��ã�a=��1��b=3��
�ʴ�Ϊ����1��3��
��2��������ɵã�
|x������1��|=|x��3|��
��ã�x=1��
�ʴ�Ϊ��1��
��3�������ϴ��ڵ�P��ʹ��P����A�͵�B�ľ���֮��Ϊ5��
������ɵã�
|x������1��|+|x��3|=5��
��ã�x1=��1.5��x2=3.5��
��4����a=��1��b=3��
��|x��a|+|x��b|=|x������1��|+|x��3|=|x+1|+|x��3|��
��x��3ʱ��|x+1|+|x��3|=x+1+x��3=2x��2��4��
����1��x��3ʱ��|x+1|+|x��3|=x+1+3��x=4��
��x����1ʱ��|x+1|+|x��3|=��x��1+3��x=��2x+2��4��
��|x+1|+|x��3|����Сֵ��4��
�ʴ�Ϊ��4��
��5����t����ʱ��P����A����B�ľ�����ȣ�
��t������1��5t��=t+3��
��ã�t=![]() ��
��
��![]() ����ʱ��P����A����B�ľ�����ȣ�
����ʱ��P����A����B�ľ�����ȣ�

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�����Ŀ����ͬѧÿ����ѧ����ѧʹ�ù������������������������������100Ԫ������˳�������![]() ��ʾ���������ϵ������
��ʾ���������ϵ������![]() ��ʾ��
��ʾ��
���� | ��� |
1 |
|
2 |
|
3 |
|
�� | �� |
(1)������ݱ����е���Ϣ���������4�γ˳��������ϵ���
(2)����д����ͬѧ�������ϵ����![]() ��˳�����
��˳�����![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
(3)�����ͬѧ�����20�γ�������������Ƕ���Ԫ��