ЬтФПФкШн
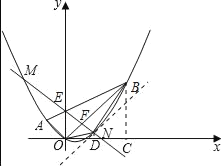
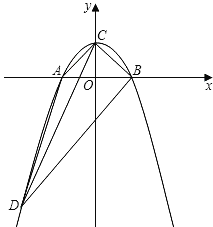
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЕФзјБъЮЊЃЈЉ2ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ6ЃЉЃЌХзЮяЯпОЙ§AЁЂOЁЂBШ§ЕуЃЌСЌНсOAЁЂOBЁЂABЃЌЯпЖЮABНЛyжсгкЕуEЃЎ
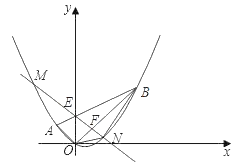
ЃЈ1ЃЉЧѓЕуEЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЕуFЮЊЯпЖЮOBЩЯЕФвЛИіЖЏЕуЃЈВЛгыЕуOЁЂBжиКЯЃЉЃЌжБЯпEFгыХзЮяЯпНЛгкMЁЂNСНЕуЃЈЕуNдкyжсгвВрЃЉЃЌСЌНсONЁЂBNЃЌЕБЕуFдкЯпЖЮOBЩЯдЫЖЏЪБЃЌЧѓЁїBONУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуNЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉEЃЈ0ЃЌ3ЃЉЃЈ2ЃЉyЃН![]() x2Љ
x2Љ![]() xЃЈ3ЃЉ
xЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіжБЯпABЕФНтЮіЪНЃЌДгЖјИљОнЕуEЕФКсзјБъЮЊ0ЃЌПЩЕУЦфзнзјБъЃЛ
ЃЈ2ЃЉИљОнХзЮяЯпЙ§дЕуЃЌПЩЩшХзЮяЯпЮЊyЃНmx2+nxЃЌДњШыAЁЂBЕФзјБъЃЌМДПЩШЗЖЈХзЮяЯпНтЮіЪНЃЛ
ЃЈ3ЃЉжЛашШЗЖЈБпOBЩЯИпЕФзюДѓжЕМДПЩЃЌЩшЙ§ЕуNЧвгыжБЯпOBЦНааЕФжБЯпНтЮіЪНЮЊyЃНx+cЃЌЕБЧвНіЕБжБЯпyЃНx+cгыХзЮяЯпyЃН![]() ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌШЗЖЈШЁЕУзюДѓЪБЕуNЕФзјБъЃЌдйгЩSЁїBONЃНSЁїOCBЉSЁїODNЉSЬнаЮNDCBЃЌМДПЩЕУГіД№АИЃЎ
ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌШЗЖЈШЁЕУзюДѓЪБЕуNЕФзјБъЃЌдйгЩSЁїBONЃНSЁїOCBЉSЁїODNЉSЬнаЮNDCBЃЌМДПЩЕУГіД№АИЃЎ
ЃЈ1ЃЉЩшЕуAЁЂBЫљдкЕФжБЯпНтЮіЪНЮЊyЃНkx+bЃЌ
дђ![]()
НтЕУЃК ![]()
МДжБЯпABЕФНтЮіЪНЮЊyЃН![]() x+3ЃЌ
x+3ЃЌ
СюxЃН0ЃЌЕУyЃН3ЃЌ
ЙЪEЃЈ0ЃЌ3ЃЉЃЎ
ЃЈ2ЃЉЁпЫљЧѓХзЮяЯпЙ§дЕуЃЌ
ЁрЩшЫљЧѓХзЮяЯпЮЊyЃНmx2+nxЃЌ
НЋЕуAЁЂBЕФзјБъДњШыЃЌЕУЃК![]()
НтЕУЃК 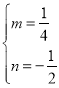
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]()
ЃЈ3ЃЉВЛФбЧѓГіжБЯпOBЕФНтЮіЪНЮЊyЃНxЃЌ
вЊЪЙЁїBONЕФУцЛ§зюДѓЃЌжЛашOBБпЩЯЕФИпзюДѓМДПЩЃЌ
ЩшЙ§ЕуNЧвгыжБЯпOBЦНааЕФжБЯпНтЮіЪНЮЊyЃНx+cЃЌ
ЕБЧвНіЕБжБЯпyЃНx+cгыХзЮяЯп![]() ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌ
ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌ
гЩ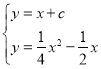 ЃЌЯћШЅyВЂећРэЕУx2Љ6xЉ4cЃН0ЃЌ
ЃЌЯћШЅyВЂећРэЕУx2Љ6xЉ4cЃН0ЃЌ
ЕБЁїЃЈЉ6ЃЉ2Љ4ЁС1ЁСЃЈЉ4cЃЉЃН0ЪБЃЌЗНГЬx2Љ6xЉ4cЃН0ЕФНтЮЊxЃН3ЃЌ
НЋxЃН3ДњШы![]() ЃЌЕУyЃН
ЃЌЕУyЃН![]() ЃЌ
ЃЌ
ЁрNЃЈ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Й§ЕуBЁЂNЗжБ№зїBCЁЭxжсгкЕуCЃЌNDЁЭxжсгкЕуDЃЌ
SЁїBONЃНSЁїOCBЉSЁїODNЉSЬнаЮNDCBЃН![]()