题目内容
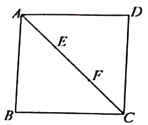
【题目】如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A. 0B. 4C. 6D. 8
【答案】D
【解析】
P点是正方形的边上的动点,我们可以先求PE+PF的最小值,然后根据PE+PF=9判断得出其中一边上P点的个数,即可解决问题.
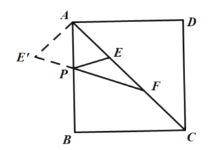
解:如图,过E点作关于AB的对称点E’,则当E’,P,F三点共线时PE+PF取最小值,
∵∠EAP=45°,
∴∠EA E’=90°,
又∵AE=EF=A E’=4,
∴PE+PF的最小值为E’F=![]() ,
,
∵满足PE+PF=9=![]() ,
,
∴在边AB上存在两个P点使PE+PF=9,
同理在其余各边上也都存在两个P点满足条件,
∴满足PE+PF=9的点P的个数是8,
故选:D.

练习册系列答案
相关题目