��Ŀ����
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P��x��y����������y���������x�IJ�y-x��Ϊ��P���������������ͼ��G�����е������������е����ֵ��Ϊͼ��G��������ֵ��
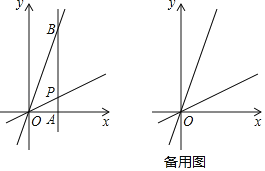
��1����A��2��6�������������Ϊ________��
��2����������y=-x2+5.x+4��������ֵ����
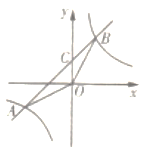
��3��ij���κ���y=-x2+bx+c��c��0����������ֵ��Ϊ-1����B���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�������������ȣ���˶��κ����Ľ���ʽ��
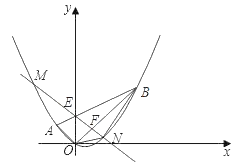
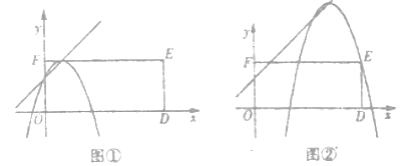
��4�����κ���y=-x2+px+q��ͼ��Ķ��������������Ϊ2��һ�κ�����ͼ���ϣ��ı���DEFO�Ǿ��Σ���E������Ϊ��7��3������OΪ����ԭ�㣬��D��x���ϵ�����x���ϣ������κ���y=-x2+px+q��ͼ������εı�ֻ����������ʱ����˶��κ����Ľ���ʽ������ֵ.
���𰸡���1��4����2��8����3��y=-x2+3x-2����4��y=-��x-5��2+7��![]()
��������
��1��������Ŀ�еĹ涨�ý��ۣ�
��2�����ݶ������y-x�ǹ���x�Ķ��κ�����Ȼ�����ö��κ���������������ۣ�
��3���������������y��Ľ���C��0��c�������B������Ϊ��-c��0��,�ѵ�B�����������κ�������ʽ�õ�b=1-c���ٽ�b=1-c������κ�������ʽ���������ֵy-x�Ĵ���ʽ��Ȼ��������ֵΪ-1���c��ֵ���̶����b��ֵ������������κ�������ʽ��
��4����������������Ϊ2��һ�κ����Ľ���ʽΪy=x+2���ɶ��κ���y=-x2+px+q��ͼ��Ķ�����ֱ��y=x+2�ϣ��ö���ʽ������κ���Ϊy=-��x-m��2+m+2.����������¶��κ�����ͼ�������ֻ���������㣺�������߶�����ֱ��y=x+2��FE�Ľ�����ʱ����ͼ�٣������������Ҳಿ�־�����Eʱ����ͼ�ڣ�.Ȼ��ֱ�ѣ�1��3������7��3���ֱ����y=-��x-m��2+m+2�����m��ֵ������������κ�������ʽ���̶����������ֵ.
��1����������������Ķ���ã�6-2=4��
��2��y-x=-x2+5x+4-x=-x2+4x+4=-��x-2��2+8������ֵ��8
��3�������⣬�õ�C������Ϊ��0��c����
�ߵ�B���C�������������ȣ�
��B��-c.0������B��-c��0������y=-x2+bx+c����0=-��-c��2+b����-c��+c��
��b=1-c��
��y=-x2+��1-c��x+c��
�߶��κ���y=-x2+��1-c��x+c��������ֵ��Ϊ-1.
��y-x=-x2+(1-c)x+c-x=-x2-cx+c��
��![]() =-1��
=-1��
��c=-2��
��b=3��
����κ����Ľ���ʽΪy=-x2+3x-2
��4���⣺���������Ϊ2��һ�κ���Ϊy=x+2��
�߶��κ���y=-x2+px+q��ͼ��Ķ�����ֱ��y=x+2�ϣ�
������κ���Ϊy=-��x-m��2+m+2��
���κ�����ͼ����������������㣬��ͼ�١��ڣ��ѣ�1��3������y=-��x-m��2+m+2����3=-��1-x��2+m+2�����m1=1��m2=2����ȥ����
����κ����Ľ���ʽΪy=-��x-1��2+3��
��y-x=-��x-1��2+3-x=-x2+x+2=-��x-![]() ��2+
��2+![]() ������ֵ��
������ֵ��![]() ��
��
�ѣ�7��3������y=-��x-m��2+m+2����3=-��7-m��2+m+2�����m1=5��m2=10����ȥ����
���κ����Ľ�����Ϊy=-��x-5��2+7��
��y-x=-(x-5)2+7-x=-x2+9x-18=-��x-![]() ��2+
��2+![]() ������ֵ��
������ֵ��![]() .
.