题目内容
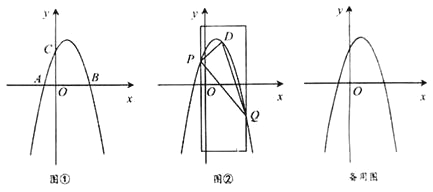
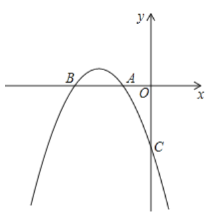
【题目】抛物线y=a(x+2)2+c与x轴交于A,B两点,与y轴负半轴交于点C,已知点A(-1,0),OB=OC.
(1)求此抛物线的解析式;
(2)若把抛物线与直线y=-x-4的交点称为抛物线的不动点,若将此抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点;
(3)Q为直线y=-x-4上一点,在此抛物线的对称轴上是否存在一点P,使得∠APB=2∠AQB,且这样的Q点有且只有一个?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1) y=x![]() 4x3;(2) m≥
4x3;(2) m≥![]() ;(3) P(2,2+
;(3) P(2,2+![]() )或(2,2
)或(2,2![]() ).
).
【解析】
(1)根据函数的解析式可以得到函数的对称轴是x=-2,则B点的坐标可以求得,求得OB的长,则C的坐标可以求得,把A、C的坐标代入函数解析式即可求得;
(2)根据平移后抛物线的顶点坐标设出抛物线的顶点式,然后根据抛物线与直线的有交点,列方程组,最后根据△≥0,求出m的取值范围;
(3)设P(-2,m),以P为圆心的圆与直线y=-x-4相切,根据切线的性质即可求解.
(1)由抛物线y=a(x+2)![]() +c可知,其对称轴为x=2,
+c可知,其对称轴为x=2,
∵点A坐标为(1,0),
∴点B坐标为(3,0),
∵OB=OC,
∴C点坐标为(0,3).
将A(1,0)、C(0,3)分别代入解析式得,
a+c=0
4a+c=3,
解得a=1,c=1
则函数解析式为y=x![]() 4x3.
4x3.
(2)由题意平移后的抛物线的解析式为y=(xm)![]() +2m,
+2m,
由x4=(xm)![]() +2m,得到:x
+2m,得到:x![]() (2m+1)x+m
(2m+1)x+m![]() 2m4=0,
2m4=0,
∵平移后的抛物线总有不动点,
∴△≥0,
∴4m![]() +4m+14(m
+4m+14(m![]() 2m4)0,
2m4)0,
解得m≥![]() .
.
(3)如图,设P(2,m),以P为圆心的圆与直线y=x4相切,切点为D,直线y=x4交抛物线的对称轴于E,则E(2,2)
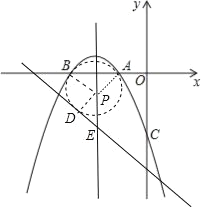
∴PE=m+2,PD=![]() PE,
PE,
∵PA=PD,
∴![]() =1+m
=1+m![]() ,
,
解得m=2±![]() ,故P(2,2+
,故P(2,2+![]() )或(2,2
)或(2,2![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案