题目内容
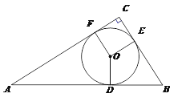
【题目】如图,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,切点为D、E、F.
(1)求证:四边形OECF是正方形;
(2)若AF=10,BE=3,求⊙O的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
根据切线的性质及正方形的判定即可求解;(2)利用切线长定理及勾股定理即可列式求解.
(1)证明:∵⊙O是Rt△ABC的内切圆,
∴OE⊥BC,OF⊥AC,OD⊥AB,
即∠C=∠CFO=∠OEC=90°,
∴四边形OECF是矩形,
又∵OE=OF,
∴矩形OECF是正方形.
(2)解:∵AF=10,BE=3,
根据切线长性质可得:AD=AF=10,BD=BE=3,
即AB=13,
设CE=FC=x,
在Rt△ABC中:
![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
即CE=FC=2,
∴OE=2,
∴![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
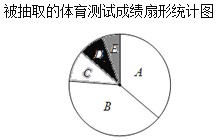
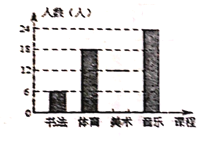
【题目】有一学校为了解九年级学生某次的体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度;
(4)已知该校九年级共有780学生,估计成绩(分)在32<x≤36之间的学生约有 人.