题目内容
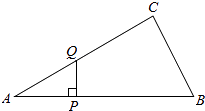
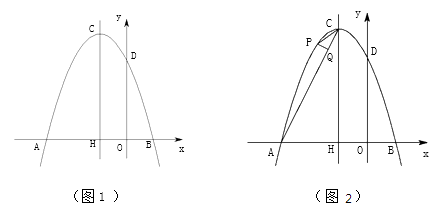
【题目】如图，一次函数y=kx+b 的图象l与坐标轴分别交于点E、F，与双曲线y=- 
（x＜0）（x＜0）交于点P（﹣1，n），且F 是PE 的中点，直线x=a与l交于点A，与双曲线交于点B（不同于A），PA=PB，则a=。
【答案】-2
【解析】将P（-1，n）代入
,得n=4,则P（-1,4），
因为F是PE的中点，过点P作PD垂直于y轴，易得△PFD≌△OFE，则F（0,2）和E（0,1）.
将F（0,2）和E（1,0）代入y=kx+b，
得
解得
则直线EF：y=-2x+2
因为x=a，则A（a,-2a+2）,B(a,
),
因为PA=PB，
则-2a2+2-
=2×4，
解得a1=-1(舍)，a2=-2.
故答案为-2.
根据反比例函数求出点P的坐标，由点F是PE的中点，可求出E，F的坐标，从而求出直线EF的解析式，用a表出示A，B的坐标，根据PA=PB列出方程求解.
练习册系列答案
相关题目
【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表． 调查结果统计表
组别 | 分组（单位：元） | 人数 |
A | 0≤x＜30 | 4 |
B | 30≤x＜60 | 16 |
C | 60≤x＜90 | a |
D | 90≤x＜120 | b |
E | x≥120 | 2 |
请根据以上图表，解答下列问题：
（1）填空：这次被调查的同学共有人，a+b= ， m=；
（2）求扇形统计图中扇形C的圆心角度数；
（3）该校共有学生1000人，请估计每月零花钱的数额x在60≤x＜120范围的人数．
