Question

【题目】如图，在平面直角坐标系内，点O为坐标原点，经过A(-2，6)的直线交x轴正半轴于点B，交y轴于点C，OB=OC，直线AD交x轴负半轴于点D，若△ABD的面积为27．

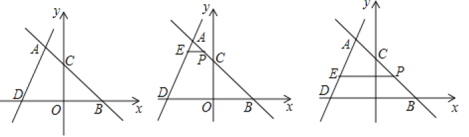
（1）求直线AD的解析式；

（2）横坐标为m的点P在AB上（不与点A，B重合），过点P作x轴的平行线交AD于点E，设PE的长为y（y≠0），求y与m之间的函数关系式并直接写出相应的m的取值范围；

（3）在（2）的条件下，在x轴上是否存在点F，使△PEF为等腰直角三角形？若存在求出点F的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）y=2x+10；（2）y=m+3（-2＜m＜4）；（3）存在，点F的坐标为(，0)或(-，0)或(-，0)

【解析】

（1）根据直线AB交x轴正半轴于点B，交y轴于点C，OB=OC，设出解析式为y=-x+n，把A的坐标代入求得n的值，从而求得B的坐标，再根据三角形的面积建立方程求出BD的值，求出OD的值，从而求出D点的坐标，直接根据待定系数法求出AD的解析式；

（2）先根据B、A的坐标求出直线AB的解析式，将P点的横坐标代入直线AB的解析式，求出P的总坐标，将P点的总坐标代入直线AD的解析式就可以求出E的横坐标，根据线段的和差关系就可以求出结论；

（3）要使△PEF为等腰直角三角形，分三种情况分别以点P、E、F为直角顶点，根据等腰直角三角形的性质求出（2）中m的值，就可以求出F点的坐标．

（1）∵OB=OC，

∴设直线AB的解析式为y=-x+n，

∵直线AB经过A（-2，6），

∴2+n=6，

∴n=4，

∴直线AB的解析式为y=-x+4，

∴B（4，0），

∴OB=4，

∵△ABD的面积为27，A（-2，6），

∴S△ABD=×BD×6=27，

∴BD=9，

∴OD=5，

∴D（-5，0），

设直线AD的解析式为y=ax+b，

∴，

解得．

∴直线AD的解析式为y=2x+10；

（2）∵点P在AB上，且横坐标为m，

∴P（m，-m+4），

∵PE∥x轴，

∴E的纵坐标为-m+4，

代入y=2x+10得，-m+4=2x+10，

解得x=，

∴E（，-m+4），

∴PE的长y=m-=m+3；

即y=m+3，（-2＜m＜4），

（3）在x轴上存在点F，使△PEF为等腰直角三角形，

①当∠FPE=90°时，如图①，

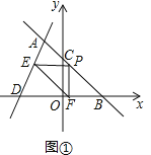
有PF=PE，PF=-m+4PE=m+3，

∴-m+4=m+3，

解得m=，此时F（，0）；

②当∠PEF=90°时，如图②，有EP=EF，EF的长等于点E的纵坐标，

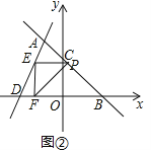
∴EF=-m+4，

∴∴-m+4=m+3，

解得：m=．

∴点E的横坐标为x==-，

∴F（-，0）；

③当∠PFE=90°时，如图③，有 FP=FE，

∴∠FPE=∠FEP．

∵∠FPE+∠EFP+∠FEP=180°，

∴∠FPE=∠FEP=45°．

作FR⊥PE，点R为垂足，

∴∠PFR=180°-∠FPE-∠PRF=45°，

∴∠PFR=∠RPF，

∴FR=PR．

同理FR=ER，

∴FR=PE．

∵点R与点E的纵坐标相同，

∴FR=-m+4，

∴-m+4=（m+3），

解得：m=，

∴PR=FR=-m+4=-+4=，

∴点F的横坐标为-=-，

∴F（-，0）．

综上，在x轴上存在点F使△PEF为等腰直角三角形，点F的坐标为（，0）或（-，0）或（-，0）．