题目内容
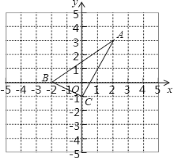
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
【答案】(1)(2)见解析;(3)![]() .
.
【解析】试题分析:
(1)根据关于y轴对称的两个点,纵坐标相等,横坐标互为相反数即可点A1,B1,C1的坐标,根据坐标描出这三个点,再顺次连接即可;
(2)连接AO,以AO为起始边,O为顶点,逆时针旋转90°,在终边上截取A2O=AO,A2即为A的旋转对应点;同理可得B2,C2,再顺次连接A2,B2,C2即可;
(3)(2)中线段 O A 扫过的图形面积即为扇形AOA2的面积,所以由题易得半径r=5,圆心角为旋转角90°,利用扇形面积公式即可计算出结果.
试题解析:
(1)由题意画图如下,图中△A1B1C1为所求三角形;

(2)由题意画图如下,图中△A2B2C2为所求三角形;
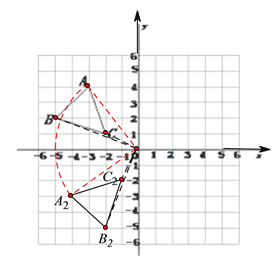
(3)如上图,线段OA扫过的图形是扇形AOA2,
∵OA=![]() ,∠A2OA=90°,
,∠A2OA=90°,
∴S扇形A2OA= ![]() .
.
即线段OA旋转过程中扫过的面积为![]() .
.

练习册系列答案
相关题目
【题目】某经销商从市场得知如下信息:
某品牌空调扇 | 某品牌电风扇 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇![]() 台,空调扇和电风扇全部销售完后获得利润为
台,空调扇和电风扇全部销售完后获得利润为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?