题目内容
一个三角形三边的长是6,8,10,同时平分这个三角形周长和面积的直线有( )条.
| A.1 | B.2 | C.3 | D.4 |
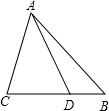
(1)若直线过△ABC的某个顶点.如图,
假设直线过点A.如果直线平分△ABC的面积,则有BN=NC,此时,AC>AB,
所以周长相等不可能.同理直线过B、C也不存在;
(2)若直线交AB、BC于点M、N.如图,
设BN=x,则BM=12-x,作MD⊥BC,
由Rt△MBD∽Rt△ABC,可得MD=
;
根据S△MBN=
MD•BN=
S△ABC,
得BN=6+
,BM=6-
,即这样的直线存在,且只有一条,
综上,同时平分这个三角形周长和面积的直线有1条.
故选A.

假设直线过点A.如果直线平分△ABC的面积,则有BN=NC,此时,AC>AB,
所以周长相等不可能.同理直线过B、C也不存在;
(2)若直线交AB、BC于点M、N.如图,
设BN=x,则BM=12-x,作MD⊥BC,

由Rt△MBD∽Rt△ABC,可得MD=
| 8(12-x) |
| 10 |
根据S△MBN=
| 1 |
| 2 |
| 1 |
| 2 |
得BN=6+
| 6 |
| 6 |
综上,同时平分这个三角形周长和面积的直线有1条.
故选A.


练习册系列答案
相关题目