题目内容
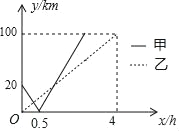
【题目】沿河岸有A,B,C三个港口,甲乙两船同时分别从AB港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
①乙船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④若设图中两者相遇的交点为P点,P点的坐标为(![]() ,
,![]() );⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是
);⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是![]() <x<2.其中正确的结论有_____.
<x<2.其中正确的结论有_____.
【答案】①②
【解析】分析:由速度=路程÷时间,可知甲、乙两船的速度,由此可判断①成立;结合图形中甲的图象可知,A、C两港距离=20+100=120km,由此可判断②成立;由时间=路程÷速度可知甲、乙两船到达C港的时间,由此可判断③不成立;由A港口比B港口离C港口多20km,结合时间=路程÷速度,得出两者相遇的时间,从而判断④不成立;由行驶过程中的路程变化可得出甲、乙两船可以相互望见时,x的取值范围,从而能判断出⑤不成立.由上述即可得出结论.
详解:甲船的速度为20÷0.5=40km/h,
乙船的速度为100÷4=25km/h,①成立;
从A港到C港全程为20+100=120km,②成立;
甲船到达C港的时间为120÷40=3(小时),
43=1小时,③不成立;
设两船相遇的时间为t小时,则有40t25t=20,
解得:![]()
即P点坐标为![]() ④不成立;
④不成立;
甲、乙两船第一次相距10km的时间为(2010)÷(4025)=![]() (小时),
(小时),
甲、乙两船第二次相距10km的时间为(20+10)÷(4025)=2(小时),
甲、乙两船第三次相距10km的时间为(10010)÷25=![]() (小时),
(小时),
即甲、乙两船可以相互望见时,x的取值范围是![]() 和
和![]() ,⑤不成立.
,⑤不成立.
故答案为:①②.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
等级 | 成绩x/分 | 频数/(人数) | 频率 |
A | 9.0≤x≤10.0 | a | m |
B | 7.0≤x<9.0 | 23 | 0.46 |
C | 6.0≤x<7.0 | b | n |
D | 0.0≤x<6.0 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)在被调查的男生中,成绩为B等级的有多少人,占被调查男生人数的多少,m 等于 多少;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.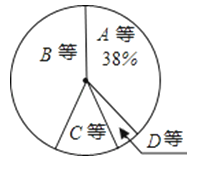
【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对![]() 对应,数5与
对应,数5与![]() 对应,数14与
对应,数14与![]() 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
第一行 | 1 | 4 | 5 | 16 | 17 | … |
第二行 | 2 | 3 | 6 | 15 | … | |
第三行 | 9 | 8 | 7 | 14 | … | |
第四行 | 10 | 11 | 12 | 13 | … | |
第五行 | … | |||||
…… |