题目内容
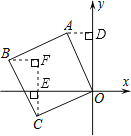
【题目】如图,平面直角坐标系中有一正方形OABC,点C的坐标为(﹣2,﹣1),则点A坐标为_____,点B坐标为_____.
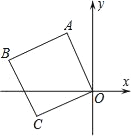
【答案】 (﹣1,2) (﹣3,1)
【解析】分析:过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,根据点C的坐标求出![]() ,再根据正方形的性质可得
,再根据正方形的性质可得![]() ,再求出∠AOD=∠COE=∠BCF,然后求出△AOD≌△COE≌△BCF,根据全等三角形对应边相等可得AD=CE=BF=1,OD=OE=CF=2,然后求解即可.
,再求出∠AOD=∠COE=∠BCF,然后求出△AOD≌△COE≌△BCF,根据全等三角形对应边相等可得AD=CE=BF=1,OD=OE=CF=2,然后求解即可.
详解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,
∵C(2,1),
∴OE=2,CE=1,
∵四边形OABC是正方形,
∴OA=OC=BC,
易求∠AOD=∠COE=∠BCF,
又∵![]()
∴△AOD≌△COE≌△BCF,
∴AD=CE=BF=1,OD=OE=CF=2,
∴点A的坐标为(1,2),EF=21=1,
点B到y轴的距离为1+2=3,
∴点B的坐标为(3,1).
故答案为:(1,2);(3,1).

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目